Definirea unei ecuații pătratice a ecuației pătratice și sinonime ale ecuației pătratice

Arabă Bulgară Chineză Croată Cehă Daneză Olandeză Engleză Estoniană Finlandeză Franceză Germană Greacă Hindi Indonezian Islandeză Italiană Japoneză Letonă Lituaniană malgașă Norvegiană Persană Poloneză Portugheză Română Rusă Sârbă Slovacă Slovenă Spaniolă Thai Turcă Vietnameză suedeză

definition - ecuația pătratică

raportează o problemă

ecuația pătratică (n.)

Dicționar analogica

ecuația pătratică (n.) ↕

în cazul în care - o variabilă liberă ,,, - coeficienți, cu

Factorul este numit termenul liber al acestei ecuații.

Împărțind ecuația de formă generală pe. puteți obține un așa-numit furnizat ecuația de gradul doi:

Rădăcinile ecuației de gradul doi din setul de numere reale

Formula generală pentru calculul rădăcinilor:

Expresia Radical se numește discriminant

la rădăcinile celor două;
la rădăcina unuia (în anumite contexte vorbesc, de asemenea, de două rădăcini egale sau identice);
la rădăcinile setului de numere reale nu.

Rădăcinile ecuației pătratice pentru chiar coeficient b

Pentru ecuațiile formei,
care este, chiar
unde
în loc de formula (1), pentru a găsi rădăcinile pot fi folosite expresie echivalentă

Această expresie este mai convenabil pentru calcule practice chiar.

Semnificația geometrică

Graficul funcției pătratică este o parabolă. Soluții (rădăcini) ale unei ecuații pătratice se numește punctul de intersecție al parabolei cu abscisa. Dacă parabolei descrisă de o funcție pătratică, nu se intersectează cu axa x, ecuația nu are rădăcini reale. Dacă parabolei se intersectează cu axa absciselor în același punct (vârful parabolei), ecuația are o radacina reala (de asemenea, spune că ecuația are două rădăcini coincident). În cazul în care parabolei intersectează axa x la două puncte, ecuația are două rădăcini reale (a se vedea. Imaginea de pe dreapta.)

În cazul în care un coeficient pozitiv al ramurii parabolei îndreptat în sus și vice-versa. În cazul în care un coeficient pozitiv (la un rezultat pozitiv, un vice-versa negativ), vârful parabolei se află în jumătatea stângă, și vice-versa.

Prepararea soluțiilor pentru

Formula poate fi obținută după cum urmează:

Ne multiplica fiecare parte, pe și adaugă:

Rădăcinile unei ecuații pătratice pe mulțimea numerelor complexe

Ecuația cu coeficienți reali

Ecuația pătratică cu coeficienți reali pot avea de la 0 la 2 rădăcini reale, în funcție de valoarea discriminantului

când două rădăcini, și ele sunt calculate conform formulei (1)
la rădăcina unuia (în anumite contexte vorbesc, de asemenea, de două rădăcini egale sau identice), de 2 ori:
pentru reale (efective) rădăcini. Există două rădăcini complexe conduc la aceeași formulă (1), (fără a extrage rădăcina unui număr negativ) sau formula

Ecuația cu coeficienți complecși

În caz complex, ecuația pătratică este rezolvată folosind aceeași formulă (1) și descrise mai sus, o variantă a acesteia, ci sunt doar două cazuri distincte: zero, discriminant (o rădăcină dublă) și nenul (două rădăcină simplă).

Aceasta induce în eroare rădăcinile unei ecuații pătratice

O ecuație pătratică a formei în care coeficientul de conducere este egal cu unitatea, apelul redus. În acest caz, formula pentru rădăcini (1) simplifică la

Aceste rădăcini înșelătoare ecuației pătratice pentru chiar coeficient b

Dacă ecuația este scris sub forma, formula este chiar mai ușor:

„Minus“ a scrie în primul rând,
Alături de el în jumătate p,
semnul „Plus-minus“ al radicalului,
Din copilărie familiar pentru noi.
Ei bine, la rădăcină, un prieten,
Cupola de toate pentru a bate joc:
p în jumătate și pătrat
Mai puțin excelent [1] q.

p. cu semnul de a lua inversă,
La doi împărțim,
Și rădăcina cu atenție
"Minus-plus" departament.
Iar la rădăcina foarte util
Jumătate din p pătrat
q Negativ - și aici este soluția,
Adică, rădăcinile ecuației.

Teorema lui Vieta

Aceasta induce în eroare suma rădăcinilor unei ecuații pătratice este coeficientul luat cu semnul opus, iar produsul a rădăcinilor este egală cu termenul constant:

În cazul general, care este de a neprivedonnogo ecuația pătratică:

a introdus poetul
Din teorema lui Vieta,
Ambele rădăcini el a demisionat -
Minus p a primit,
Un produs al rădăcinilor
Ea dă q din ecuație.

Descompunerea ecuației pătratice în factori

Dacă știm ambele rădăcini ale ecuației pătratice, acesta poate fi descompus prin formula

Dacă discriminante este zero raportul devine una dintre variantele de realizare cu formula sumă pătrată sau diferență.

Definirea unei ecuații pătratice a ecuației pătratice și sinonime ale ecuației pătratice

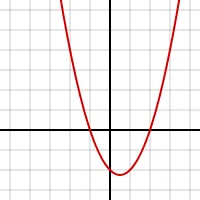
Pentru funcția pătratică:
f (x) = x 2 - x - 2 = (x + 1) (x - 2) a unei variabile x reale. x -coordinates a punctelor în care graficul intersecteaza x -axis, x = -1 și x = 2, sunt soluțiile ecuației pătratice: x 2 - x - 2 = 0.

Ecuațiile reductibile la pătratic

algebric

Ecuația a formei este o ecuație care poate fi redus la pătrat.

În general, se rezolvă prin înlocuirea c urmată de o soluție a ecuației pătratice.

De asemenea, în cazul în care decizia este posibil să se facă fără un înlocuitor, determinată combinație de două ecuații:

Dacă, atunci ecuația devine:

Aceasta se numește ecuație biquadratic [2].

diferențială

substituție reduce la ecuația pătratică caracteristică:

Dacă soluțiile acestei ecuații nu sunt egale, atunci soluția generală este de forma:

, unde - constantele arbitrare.

Pentru rădăcini complexe pot rescrie soluția generală folosind formula lui Euler:

Dacă soluțiile ecuației caracteristice sunt aceleași, soluția generală poate fi scrisă ca:

Ecuațiile de acest tip sunt adesea găsite într-o mare varietate de probleme în matematică și fizică, de exemplu, în teoria oscilațiilor și teoria circuitelor de curent alternativ.

notițe

↑ cealaltă opțiune - „nefericită“
↑ Dicționarul Enciclopedic de Matematică. - M. sovietic Enciclopedia. - 1988.