Definirea moment de inerție fizicheskogomayatnika
DEFINIREA moment de inerție
Scopul lucrării. familiarizarea cu pendulul fizic și determinarea momentului său de inerție față de axa de rotație. Studiul dependenței momentului de inerție al masei pendulului asupra distribuției spațiale.
Instrumente și accesorii. pendul fizic cu suportul de suspensie, prisme metalice pentru detectarea poziției centrului de greutate al pendulului cronometrului.
pendulului fizic (Figura 1) este orice solid, care se realizează sub influența oscilațiilor gravimetrice în jurul unei axe fixe orizontală (A), care nu trece prin centrul de greutate (C). punct suspensie pendul este un centru de rotație.

Fig.1. compus cu pendul
Când devierea pendulului din poziția de echilibru la un unghi ia naștere cuplul generat de gravitate:
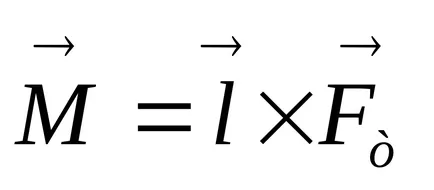
,
unde l - distanța dintre punctul de suspensie și centrul de greutate al pendulului (semnul E con datorită faptului că momentul forței M are o astfel de direcție care tinde să se întoarcă pendulului Xia la echilibru, adică reduce unghiul ).
Pentru unghiuri mici de deflecție
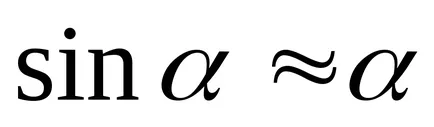
Pe de altă parte, momentul forței de readucere poate fi scrisă ca:
I - momentul de inerție al pendulului
i - accelerația unghiulară.
De la (1) și (2) pot fi obținute:
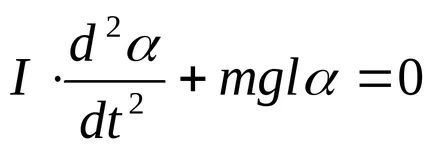
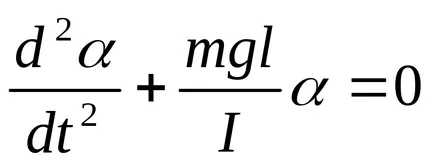
Ecuația (4), - o ecuație diferențială liniară de ordinul 2. Soluția lui este expresia.
Având în vedere ecuația (3) perioada de mici oscilații ale unui pendul fizic poate fi scrisă ca:
unde
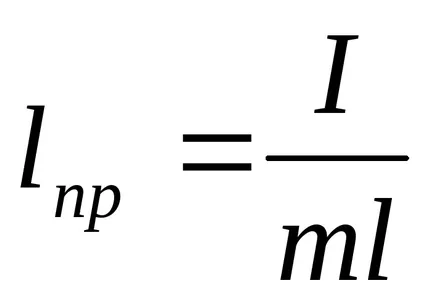
Din formula (5) pot fi exprimate în momentul fizic de inerție al pendulului în raport cu axa de rotație
Găsirea prin măsurarea m, l și T. posibil prin formula (6), pentru a calcula un moment pendul fizic de inerție o anumită axă de rotație.
Această lucrare folosește un pendul fizic (2), care este o tijă de oțel, pe care sunt fixate două lintea masive din oțel (A1 și A2) și prisme de referință pentru suspensie (P1 și P2). Momentul de inerție al tijei de pendul va ieși din momentele de inerție, linte si prisme:
.
Momentul de inerție al tijei poate fi calculată folosind teorema lui Steiner:
,
unde I0 - momentul de inerție al tijei în raport cu o axă care trece prin centrul de greutate.
d - distanța de la centrul arborelui de greutate la punctul de suspendare.
Momentele de linte inerție și prisme poate fi aproximativ calculată pentru puncte de masă. Apoi, în momentul de inerție al pendulului poate fi scris ca:
unde
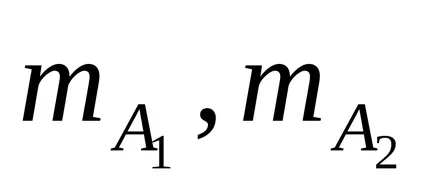
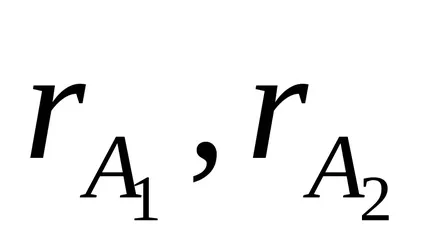
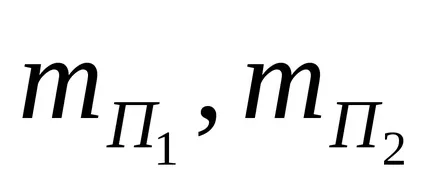
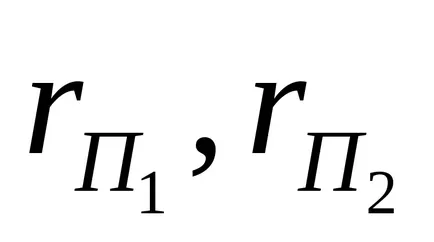
pentru că numai pe o linte A1 se mută la condițiile de performanță. schimbarea va fi doar un moment de inerție
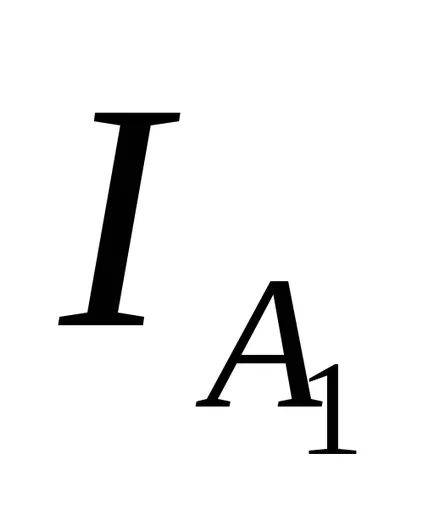
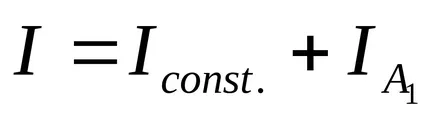
pendulului fizic (figura 2), utilizat în această lucrare este o tijă de oțel (P) pe care sunt fixate două lintea masive din oțel (A1 și A2) și prisme de referință pentru suspensie (P1 și P2). Pendulul este suspendat pe suport.
Prin mutarea una dintre lintea poate schimba momentul de inerție al pendulului în raport cu punctul de suspensie (axa de rotație).
Centrul de greutate al pendulului pendulului de echilibrare determinat pe o prismă specială nervură orizontală (figura 3). Pe tija pendulului inelului de tăiere acoperit cu 10 mm care servește pentru a determina cu exactitate distanța dintre centrul de greutate și axa de rotație, fără a utiliza o riglă. A1 lentil mică deplasare de-a lungul axului poate fi realizat că distanța L din punctul de suspensie la centrul de greutate egală cu un număr întreg de centimetri, calculată pe scara pe tulpină.
Ordinea de performanță.
Determinați poziția centrului de greutate al pendulului.
a) Se îndepărtează pendulul din suport și puneți-l într-o poziție orizontală, pe un P3 special prismă (figura 3), astfel încât să fie în echilibru. Poziția exactă a echilibrului se realizează prin deplasarea unui mic Linte A1.
Figura 3. pendul de echilibrare
b) Pe o scală pentru măsurarea pendulului l - distanța de la punctul de suspensie (marginea prismei P1) la centrul de greutate al pendulului (marginea superioară a P3 prismei).
c) Pe o scală a pendulului pentru a măsura distanța
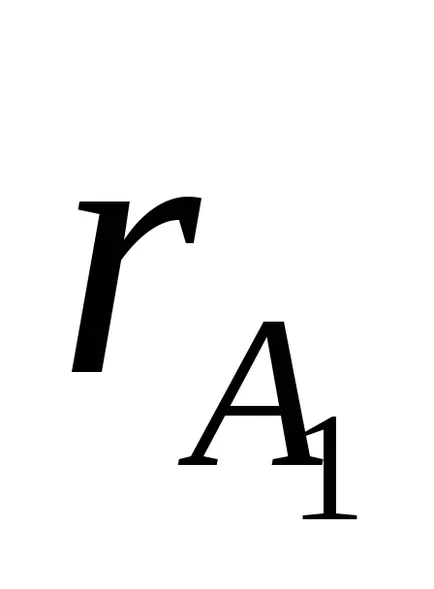
2. Se determină fizic perioada de oscilație pendul.
a) Setați P1 pendula prism pe suportul (Figura 2)
b) determinarea timpului total de 50 - 100 oscilației pendulului. Se înregistrează timpul t n și numărul de oscilații ale pendulului.
c) determină perioada unei oscilații cu pendul fizic în conformitate cu formula:
3. Scoateți suportul bascula. linte A1 muta câțiva centimetri într-o nouă poziție și se repetă experiența. Măsurătorile trebuie efectuate cel puțin trei poziții diferite în raport cu punctul A1 suspensie lintea.
4. Conform formulei (6) pentru a calcula momentul de inerție al pendulului fizic Iop.
5. Se calculează momentul de inerție relativă a erorii pentru unul dintre cazurile examinate de formula:
magnitudine T și instrumente de precizie clasa l definite.
6. Găsiți eroarea absolută
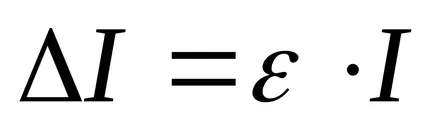
Scris în tabel ca rezultat final
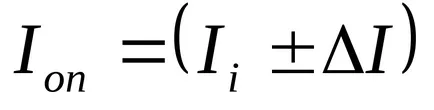
7. Conform formulei (8), pentru a calcula momentul de inerție al pendulului Iteor pentru fiecare caz.
8. Comparați rezultatele și Iop Iteor. prin calcularea raportului dintre:
Pentru a trage o concluzie despre cât de mare a valorilor obținute diferență și motivele pentru discrepanțe.
Rezultatele măsurătorilor și a calculelor
Ceea ce se numește o oscilație armonică?
Care este perioada de oscilație?
Formulele de calcul perioada unei oscilații cu pendul fizic.
Ce este inerție? Care este momentul de inerție al aditivului?
Cum de a calcula momentul de inerție în jurul axei nu trece prin centrul de greutate?
Ia formula de calcul a momentului de inerție al pendulului fizic.
1. Savelev I. V. Curs de fizică generală: formare. ajutor pentru colegii tehnice :. 3 tone Vol.1: Mecanică. Fizica moleculara. - 3rd ed. Corr. - M. Nauka, 1986. - 432s.
2. Detlaf A. A. Yavorsky BM Fizică Curs: formare. ajutor pentru colegii tehnice. - M. Școala Superioară, 1989. - 607 p. - piese. decret. a. 588-603.
3. practică de laborator în fizică: Manualelor. manual pentru studenții de colegii tehnice / BF Alexeev KA Barsukov I. A. Voytsehovskaya, etc.; Ed. KA Barsukov Yu. I. Uhanova. - M. Executiv. Școala 1988. - 351 cu. il.