Cum se citește matricea
Termenul „matrice“ este cunoscută în algebra liniară. Înainte de a descrie operațiile permise pe matrici, este necesar să se introducă definiția sa. Matricea este un tabel dreptunghiular de numere care cuprinde un număr de rânduri m și un număr n de coloane. Dacă m = n, atunci matricea se numește un pătrat. Matricile sunt de obicei notate cu majuscule, cum ar fi A sau A = (aij), unde (aij) - element de matrice, i - numărul liniei, j - indicele coloanei. Având în vedere cele două matrici A = (aij) și B = (bij) având aceeași dimensiune m * n.

instrucție
Matricea Suma A = (aij) și B = (bij) este matricea C = (cij) din aceeași dimensiune. în care elementele sale sunt definite prin cij cij = aij + bij (i = 1, 2, ..., j = 1 m-, 2, ..., n).
matrici de adiție are următoarele proprietăți:
1. A + B = B + A
2. (A + B) + C = A + (B + C)
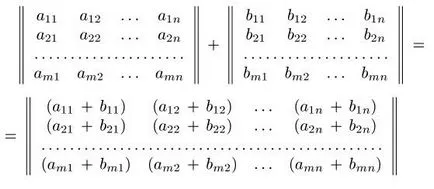
Produsul a matricei A = (aij) la un număr real. Este matricea C = (cij), în care elementele sale sunt definite prin cij cij =. * Aij (i = 1, 2, ..., j = 1 m-, 2, ..., n).
Înmulțirea numărului matricei are următoarele proprietăți:
1. (??) A =? (? A). și. - numere reale,
2. (A + B) =? A +? B. - numărul real,
3. (? +?) = B? B +? B. și. - numere reale.
Introducerea unei matrice de multiplicare cu un scalar, puteți introduce operația matrice de scădere. Diferența matricile A și B este o matrice C, care poate fi calculată conform regulii:
C = A + (-1) * B
produs Matrix. O matrice poate fi multiplicat cu matricea B, când numărul de coloane ale matricei A este numărul de rânduri ale matricei B.
Produsul a matricei A = (aij) de dimensiune m * n în matricea B = (bij) de dimensiune n * p este matricea C = (cij) de dimensiuni m * p, în care elementele cij sunt definite prin formula cij = AI1 * b1j + AI2 * b2j + ... + ain * bnj (i = 1, 2, ..., j = 1 m-, 2, ..., p).
Figura prezintă un exemplu al unui produs de matrici de dimensiune 2 * 2.
Matricea produs are următoarele proprietăți:
1. (A * B) * C = A * (B * C)
2. (A + B) * C = A * C + B * C sau A * (B + C) = A * B + A * C
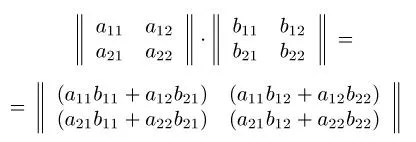
Sfat 2: Cum se calculează matricea inversă
Matricea este considerată a fi inversul matricei A, în cazul în care formează înmulțirea matricei unitate E. Termenul „matrice inverse“ există numai pentru o matrice pătrată, adică Matrix „doi câte doi“, „trei pe trei“, etc. Matricea inversă este notată cu superscript „-1“.

instrucție
Pentru a găsi inversa unei matrice, se folosește formula:
A ^ (- 1) = 1 / | A | x A ^ m, unde
| A | - determinantul A,
A ^ t - matricea transpusă a cofactori, ale elementelor corespunzătoare ale matricei A.
Înainte de a trece la determinarea matricei inverse, se calculează determinant. Matrix „doi câte doi“ determinant se calculează după cum urmează: | A | = A11a22-a12a21. Determinantul orice matrice pătratică poate fi definită prin formula: | A | = (- 1) * (1 + j) x x a1j Mj unde Mj - suplimentar minor la a1j elementului. De exemplu, matricea „doi câte doi“ cu elemente din primul rând a11 = 1, a12 = 2 pentru al doilea rând 3 = a21, a22 = 4 va fi egal cu | A | = 1h4-2h3 = -2. Rețineți că, dacă o matrice dată determinantul este zero, matricea inversă pentru ea există.
Apoi găsi o matrice de minori. Pentru această cruce mental coloană și rând, în care elementul de luat în considerare. Numărul rămas va fi minor al elementului, acesta ar trebui să fie scris într-o matrice de minori. În acest exemplu, pentru elementul a11 minor = 1 este M11 = 4 A12 = 2 - 3, = M12 pentru a21 = 3 - 2 = M21 pentru a22 = 4 - M22 = 1.
În continuare, găsiți matricea de cofactori. În acest scop, schimbarea semn și elementele sunt pe diagonală: și A12 și 21. Astfel, elementele matricei sunt egale cu: 4 = a11 și a12 = -3, -2 = a21, a22 = 1.
Apoi găsește o matrice transpusa de cofactori de A ^ T. Pentru acest cofactori matrice linie scrie în coloanele matricei transpuse. În acest exemplu, matricea transpusa va avea următoarele elemente: 4 = a11 și a12 = -2, -3 = a21, a22 = 1.
Apoi substitui valorile obținute în formula originală. Matricea inversă A * (- 1) este egală cu produsul dintre -1/2 = 4 elemente a11, a12 = -2, -3 = a21, a22 = 1. Cu alte cuvinte, elementele matricei inverse sunt egale cu: a11 = -2, a12 = 1, a21 = 1,5 a22 = -0.5.