Cum de a găsi suprafața unui cerc, pătrat, triunghi
Cum de a găsi suprafața unui cerc?
Circumferința - o curbă închisă plan din care fiecare punct este echidistant față de un punct dat (centru), situată în același plan ca și curba.
Cercul - o parte a planului delimitat de un cerc.
Raza - segmentul de linie care leagă centrul cercului cu un punct al ei, precum și lungimea acestui segment. De obicei, oboznachaetsyaR.
Diametrul - un segment de linie care leagă perechea cea mai la distanță unul de altul circumferențial de puncte, iar lungimea acestui interval. Diametrul trece întotdeauna prin centrul cercului. De obicei, oboznachaetsyaD Ilio. Diametru egal cu de două ori raza cercului: D = 2R, R = D / 2.
Raportul dintre circumferința și diametrul său este același pentru toate circumferințe. Această relație este un număr transcendental, care este notată cu litera grecească pi: π = 3,14159.

Cum de a găsi aria unui triunghi?
Triangle - o figură geometrică plană delimitată de trei lungimi de perechi de linii intersectate. Punctele de intersecție nazyvayutsyavershinami treugolinika și desemnat în general cu litere latine majuscule: A, B, C. Velichinyuglov la nodurile din care se intersectează liniile corespunzătoare sunt, de obicei notate cu literele grecești: α, β, y. Opuse colțuri segmente de linie care delimitează nazyvayutsyarebrami triunghi (laturile) ale triunghiului și sunt desemnate respectiv a, b, c.
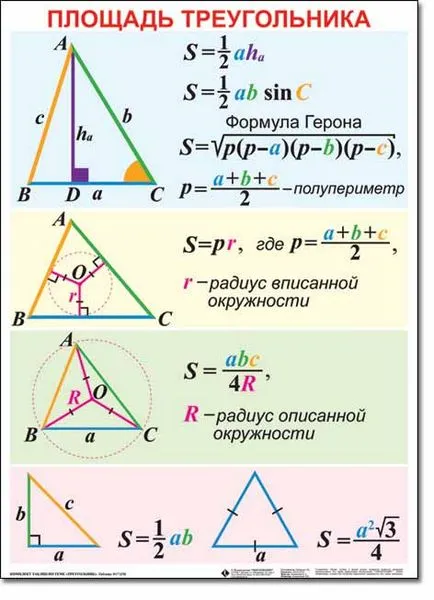
Mai jos sunt formule prin care se pot găsi zona S triunghiului cu nodurile A, B, C, valorile corespunzătoare ale unghiurile a, β, γ și laturile opuse ale acestora a, b, c:
S = a · b · sin (γ) / 2 = a · c · sin (β) / 2 = b · c · sin (α) / 2,
S = a · păcat 2 (β) · sin (γ) / (2 · sin (β + γ),
S = √ (p · (p - a) · (p - b) · (p - c)) (formula lui Heron) unde √ (.) - desemnarea rădăcinii pătrate, p = (a + b + c) / 2 - semiperimetrul triunghi.
S = a · ha / 2 = b · hb / 2 = c · hc / 2. unde ha - înălțimea redusă de la un vârf de la A partea a, hb - de la B la apex lateral b, hc - pornește din punctul C la partea c.
S = r · p. unde r - raza incircle, p = (a + b + c) / 2 - jumătate de perimetru al triunghiului.
S = a · b · c / 4R, unde R - raza cercului circumscris în jurul triunghiului.
(. X3 y3) Daca coordonatele carteziene sunt puncte specificate în planul A (. X1 y1), B (. X2 y2) și C, zona S poate fi găsit prin următoarea ecuație (determinantul prin matrici de ordinul doi pentru a coordona diferențele):
S = | (x1 - x3) · (y2 - y3) - (x2 - x3) · (y1 - y3) | / 2. în cazul în care |. | - desemnarea modulului. Această formulă este derivat din expresia produsului vectorial al celor doi vectori într-un plan care este în mărime egală cu determinantul coordonatele lor.
Cum de a găsi aria unui triunghi dreptunghic?
Se numește triunghi dreptunghiular. un colț, care este de 90 ° (un drept). Deoarece suma unghiurilor unui triunghi este de 180 °, un unghi drept al triunghiului poate fi doar unul.
Mai jos sunt formule de calcul formula S. zona spetsificheskikie pentru triunghiuri dreptunghiulare. Legendă: a - lungimea ipotenuzei (partea opusă unghi drept), un. b - lungimea picioarelor (laturile adiacente unghiul drept), a. β - unghiuri opuse aceste cantități cateta (α + β = 90 °).
Pentru două catete: S = a · b / 2
Prin catete si ipotenuza: S = a · sqrt (c 2 - a 2) / 2 = b · sqrt (c 2 - b 2) / 2.
unde sqrt (.) - desemnarea rădăcinii pătrate
H um pentru a găsi zona de pătrat?
Piața (din quadratus latină -. Patrulateră) - dreapta pătrat pe care toate laturile și unghiurile sunt egale. Poate fi definit ca un dreptunghi în care două laturi adiacente sunt egale între ele, sau ca un romb, în care toate unghiurile sunt unghiuri drepte.
Simetria. Pătratul are cea mai mare simetrie dintre toate patrulatere. Are:
- Patru axe de două ori simetrie (figura plan care este reflecții echivalente), dintre care două se extind de-a lungul diagonalelor unui pătrat, iar celelalte două - laturile paralele;
- a patra axă de simetrie (care trece prin centrul unui pătrat perpendicular pe planul său).
Diagonal. Pătratul are două diagonale de conectare vârfuri neadiacente. Diagonalei pătratului sunt Bisectoarele unghiurilor sale se intersectează în centrul pătrat în unghi drept una față de cealaltă și împărțiți în jumătate. Fiecare diagonală împarte pătrat în două triunghiuri isoscele dreapta. Două diagonalele împreună împărți pătrat în patru triunghiuri isoscele dreapta.
Dacă notăm partea de pătrat a. lungimea d diagonală se calculează în conformitate cu teorema lui Pitagora:
Înscrisă și cercurile circumscrise. Înscrisă într-un cerc pătrat este tangentă la mijlocul pieței pe toate laturile și are o rază r. egală cu jumătate din latura de pătrat a. Descrisă un pătrat în jurul circumferinței trece prin toate nodurile sale și are o rază R. egală cu jumătate din lungimea diagonalei unui pătrat d:
Perimetrul și zona. Perimetrul P sum pătrat de lungimile cele patru laturi ale sale. Zona S este egală cu pătratul pătratul lungimea laturilor sale:
P = 4a = 8r = 2√2 · R,
S = a 2 = 4r 2 = 2R 2.
Cum de a găsi aria unui trapez?
Trapez - patrulater în care cele două laturi paralele (baza trapezului), în timp ce ceilalți - non-paralele (laturile laterale ale trapezului). Segmentul care conectează mijlocul laturilor, se numește linia de mijloc a trapez.