Cum de a construi un set de fractal Apollo

Partea 2 din 2: Construcția Apollo Edit

O mulțime de Apollo ia forma unui design frumos fractal de la declin la o rată de ture. Matematic multe Apollo infinit de complex, dar dacă utilizați un program de calculator, sau instrumente tradiționale de desen, va ajunge în cele din urmă la punctul în care ar fi imposibil de a desena un cerc mai mic. Rețineți că, mai precis desena un cerc, cu atât mai mult se vor întâlni o varietate de Apollo.

Începeți cu un cerc mare. Prima sarcină - doar desena un cerc mare, perfect netedă. Cu cât mai mare cerc, cu atât mai dificil poate fi fractală dvs., astfel încât încerca să se construiască un cerc, care permite dimensiunea hârtiei, sau astfel încât să poată vedea în întregime pe ecran într-un program de grafică.

Desenați un cerc mai mic în primul cerc, care va atinge la un moment dat. Deci, desena un cerc în interiorul cercului primei noastre, acesta va fi mai mică decât principalul, dar încă destul de mare. Dimensiunea exactă a doilea cerc este de până la tine, deoarece nu există nici o sumă fixă. Cu toate acestea, să atragă un al doilea cerc, astfel încât este nevoie de jumătate din cercul principal. Cu alte cuvinte, centrul său - este raza cercului de mijloc mai mare.

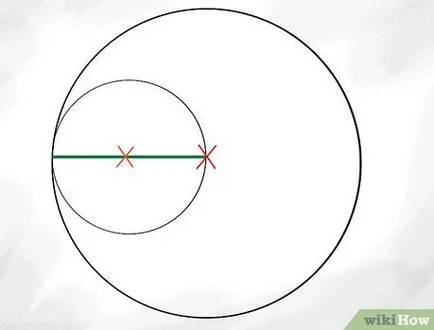
• Rețineți că setul Apollo toate cercurile sunt tangente între ele. Dacă utilizați în construirea unei cercuri busolă recrea acest efect prin plasarea capătul ascuțit al unei busole în mijlocul razei cercului de bază, și ajustând creion compas, astfel încât acesta atinge doar marginea cercului, apoi desena un cerc interior mai mic.

Desenați un cerc aproape identic la circumferința interioară. Deci, să atragă un alt cerc de lângă primul. Cercul trebuie să fie tangent la ambele cercuri: exterior mai și interior inferior, ceea ce înseamnă că atât circumferința internă învecina exact în centrul mare.

Aplicarea teoriei lui Descartes, pentru a calcula dimensiunea acestor cercuri. Pentru un moment, stop desen. Acum, că avem cele trei cercuri din fractal, putem folosi teorema lui Descartes pentru a găsi raza cercului următor, care va atrage. Notă Descartes ecuație teorema d = a + b + c ± 2 (√ (a x b + b × c + c × a)). unde a, b și c este curbura a trei cercuri tangente și d - curbura cercului tangent la toate trei. Prin urmare, pentru a găsi raza următoarea rundă noastre, să calculeze curbura fiecare din cercul nostru existent, până când vom putea găsi curbura cercului următor și apoi se calculează raza sa.

• Să definim raza circumferinței exterioare ca 1. Deoarece celelalte cercuri sunt în interiorul acestuia, avem de-a face cu „intern“ curbat (în loc de externe), și, prin urmare, noi știm că este negativ. - 1 / r = -1/1 = -1. Deoarece curbura cercului mare este egal cu -1.
• Raza cercului mai mic este jumătate din raza mare, adică 1/2. Deoarece acestea circumferință în contact unul cu celălalt și cercul principal extern, avem de a face cu curbura externă pozitivă. 1 / (1/2) = 2. Prin urmare, curbura cercului mai mic este egal cu 2.
• Acum știm că o = -1, b = 2 și c = 2 în teorema noastră ecuația lui Descartes. Să se calculeze d:
  • d = a + b + c ± 2 (√ (a x b + b × c + c × a))
  • d = -1 + 2 + 2 ± 2 (√ (-1 x 2 + 2 x 2 + 2 x -1))
  • d = -1 + 2 + 2 ± 2 (√ (-2 + -2 + 4))
  • d = -1 + 2 + 2 ± 0
  • d = -1 + 2 + 2
  • d = 3. Curbura următor circumferential 3. Deoarece 3 = 1 / r, raza cercului este egală cu 1/3.

Desenați următoarele două cercuri. Pentru a desena următoarele două cercuri, folosind raza pe care tocmai l-ați găsit. Nu uitați că aceste cercuri sunt tangente la cei a căror curbură a fost utilizată pentru calcularea teorema cartezian. Cu alte cuvinte, ei vor atinge și cercurile primare și secundare. Pentru aceste cercuri atingând celelalte trei, trebuie să le atragă în zona deschisă de mai sus și mai jos în runda principală.

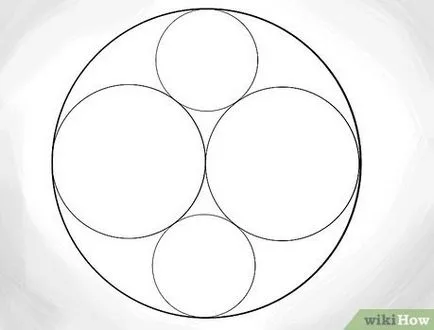
• Rețineți că raza acestor cercuri este egală cu 1/3. Se măsoară 1/3 din muchia circumferință exterioară, și apoi trage unul nou. Ar trebui să fie tangentă la toate cele trei cercuri din apropiere.

Astfel, păstrează adăugarea de circumferință. Din moment ce acestea sunt fractali, multe Apollo infinit de complex. Acest lucru înseamnă că puteți adăuga cercul mai mici și mai mici la baza fractale. Tu sunt limitate doar de acuratețea instrumentelor dvs. (sau, dacă utilizați computerul, capacitatea de a crește programul grafic). Fiecare cerc, indiferent cât de mic ar fi, trebuie să fie tangent la celelalte trei. Pentru a desena un cerc de fiecare utilizare ulterioară a curburii trei cercuri tangente la ea pentru teorema lui Descartes. Apoi, utilizați răspunsul desena în mod corect un cerc nou.

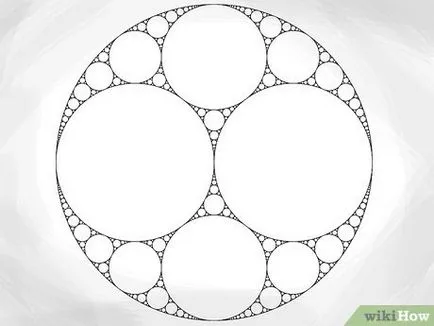
• Rețineți că setul pe care l-am ales pentru a construi, simetrice, astfel încât raza unui cerc este aceeași ca și raza unui cerc identic cu acesta. Cu toate acestea, nu toate seturile Apollo simetrice.
• Să ne uităm la un alt exemplu. Să presupunem că, după construirea ultimele două cercuri, dorim să atragem tangenta cerc pentru a treia pereche noastră și cercul de bază. Curbura acestor cercuri este de 3, 2 și respectiv 1. Acum includem aceste numere în teorema carteziană, considerând că a = -1, b = 2 și c = 3:
  • d = a + b + c ± 2 (√ (a x b + b × c + c × a))
  • d = -1 + 2 + 3 ± 2 (√ (-1 x 2 + 2 x 3 + 3 x -1))
  • d = -1 + 2 + 3 ± 2 (√ (-2 + -3 + 6))
  • d = -1 + 2 + 3 ± 2 (√ (1))
  • d = 2, 6. Avem două răspunsuri! Cu toate acestea, știm că noul nostru cerc va fi mai mică decât tangenta la ea, astfel încât va face sens doar pentru a evalua curbura 6 (o raza de 1/6).
  • Un alt răspuns, 2, de fapt, se referă la un cerc ipotetic pe „cealaltă parte“ a punctului de tangenta al doilea și al treilea cerc. Acest cerc este tangent la ambele aceste cercuri, și principalul, dar ea va traversa cele ale cercului, pe care tocmai l-am tras, astfel încât să puteți ignora acest răspuns.

Ca un test, încercați să construiască un set asimetric Apollo, modificarea dimensiunii celui de al doilea cerc. Toate seturile Apollo încep să construiască cu aceeași - cu o circumferință exterioară mare, care este fractal limită. Cu toate acestea, nu este nevoie să fie egală cu raza celui de al doilea cerc al primei reprize. Tocmai ne-am decis să ia aceste numere pentru simplitate și ușurința înțelegerii. Pentru distracție, încercați să construiască un nou set de al doilea cerc de o dimensiune diferită - aceasta va conduce la noi directii in cercetare.

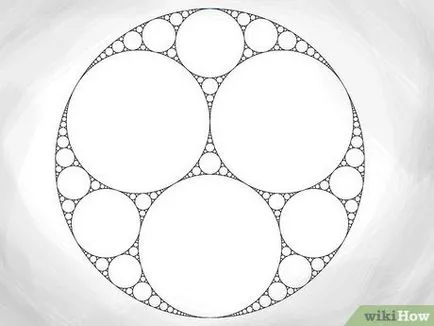
• După ce a construit al doilea cerc (indiferent de dimensiunea acesteia), următoarea acțiune ar trebui să fie pentru a construi una (sau mai multe) cercului care este tangent la al doilea și la principalele circumferințele exterioare - nu numai metoda corectă cu privire la modul de a construi. Apoi, puteți utiliza teorema lui Descartes pentru a determina raza următoarelor cercuri, așa cum se arată mai sus.