Criterii de matrice și productivitatea

Există mai multe criterii de performanță ale matricei A.

1. matricea A este productivă, în cazul în care cantitățile maxime ale elementelor coloanelor nu depășește unitatea, și cel puțin una dintre coloanele elementelor strict mai putin una.

2. Pentru a asigura un rezultat pozitiv final de eliberare a tuturor sectoarelor este necesar și suficient ca una dintre următoarele condiții:

3. Determinantul matricei (E - A) nu este egal cu zero, adică matrice (E-A) are o matrice inversă (E - A) -1.

4. Cea mai mare valoare proprie de modul A, și anume, soluție a ecuației | # 955; E - A | = 0 este strict mai mică decât unu.

5. Toți minorii principali (E - A) de ordinul de la 1 la n, sunt pozitive.

Matricea A este elemente non-negativ și care satisface criteriul eficienței (pentru orice sumă a elementelor j coloană Σaij ≤ 1.

II. Definim matricea coeficienților cheltuielilor complete, cu precizie, folosind non-degenerate formule de inversiune matrice.

Coeficientul costurilor totale (bij) arată cantitatea de produs i-a industriei de a produce, de a lua în considerare costurile directe și indirecte ale acestei unități de producție pentru a obține produsul final de ramura j-a.

Să reflecte costurile totale ale utilizării resurselor la toate etapele de producție și trebuie să fie egală cu suma costurilor directe și indirecte ale tuturor etapelor anterioare de producție.

a) Găsiți matricea (E-A):

b) Calculati matricea inversă (E-A) -1:

Scriem matricea sub formă de:

Determinantul este nenul, deci matricea este non-singular, și este posibil să se găsească matricea inversă -1.

Să ne găsim cofactori.

Verificați dacă principalul echilibru relație formulă raportul echilibru primar Σyi = Σzj = 600

Lăsați compania va produce unitățile de bunuri din primul tip și al doilea tip de unități vândute. Apoi restricțiile privind consumul de materii prime, forței de muncă și echipament poate fi scris ca:

Dimensiunea profitul obținut din vânzarea de toate produsele vor fi. Apoi, un model matematic al acestei probleme poate fi scrisă ca:

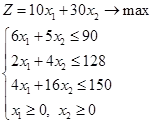
Noi rezolva problema metodei simplex grafic rezultat.

Este necesar să se găsească valoarea maximă a funcției obiectiv F = 10x1 + 30x2 → max, în cazul în care constrângerile de sistem:

Noi construim o regiune fezabilă, și anume, rezolva grafic un sistem de inegalități. Pentru aceasta vom construi fiecare linie și definesc jumătate de planul definit de inegalitățile (semiplanului sunt desemnate printr-un prim).

Intersecția semiplanuri va fi regiunea ale cărei coordonate puncte satisfac constrângerile de inegalitate ale problemei sistemului.
Notăm limita soluțiilor unui poligon.

Luați în considerare problema funcției obiectiv F = 10x1 + 30x2 → max.
Constructul linie corespunzătoare valorii funcției F = 0: F = 10x1 + 30x2 = 0. Gradientul vector al coeficienților funcției obiectiv, specifică o direcție de maximizare F (X). Pornirea vectorului - punctul (0, 0), capătul - punctul (10; 30). Să trecem această linie într-un mod paralel. Din moment ce ne interesează soluția maximă, așa că vom merge direct la ultima atingere zona desemnată. În graficul de această linie este indicat printr-o linie punctată.

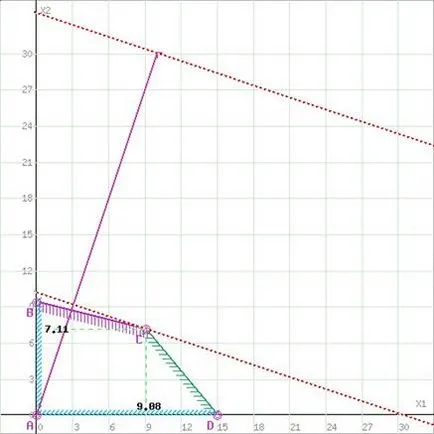
F Direct (x) = const intersectează la punctul C. Din punctul C se obține prin intersecția liniilor (1) și (3). coordonatele sale satisfac ecuațiile acestor linii:
6x1 + 5x2 = 90
4x1 + 16x2 = 150
După ce a rezolvat sistemul de ecuații, obținem: x1 = 9.0789, x2 = 7.1053
Cum vom găsi valoarea maximă a funcției obiectiv:
F (X) = 10 * 30 + 9.0789 * 7.1053 = 303.9474