cristale ionice - studopediya
Astfel de substanțe sunt formate printr-o legătură chimică, care se bazează pe interacțiunile electrostatice dintre ionii. legătură ionică (de tip polaritate - heteropolar) este limitată în principal la binare NaCl sisteme de tip (ris.1.10 a), care este instalat între atomii elementelor care au cea mai mare afinitate pentru electroni, pe de o parte, și atomii de elemente care au cel mai scăzut potențial ionizare, pe de altă parte. In formarea unui cristal ionic, vecinii cei mai apropiați ai ionului sunt ionii de semn opus. În raportul cel mai favorabil al mărimii ionilor pozitivi și negativi, se ating reciproc, și a obținut o densitate extrem de mare de ambalare. O mică schimbare în distanța inter-ion în direcția reducerii sale de echilibru dă naștere la forțe repulsive ale cojilor de electroni.
Gradul de ionizare al atomilor care formează cristale ionice, de multe ori, astfel încât învelișul de electroni al ionilor corespund electroni cochilii caracteristice atomilor de gaz inert. O estimare aproximativă a energiei de legătură poate fi făcută presupunând că cea mai mare parte din aceasta se datorează Coulomb (adică electrostatice) interacțiuni. De exemplu, într-o NaCl distanta de cristal dintre ionii pozitivi și negativi adiacente este de aproximativ 0,28 nm, care dă valoarea energiei potențiale asociate cu atracția reciprocă a unei perechi de ioni, circa 5,1 eV. Valoarea energetică determinată experimental de 7,9 eV NaCI per moleculă. Astfel, ambele de același ordin de mărime și permite utilizarea acestei abordări pentru calcule mai exacte.
legături ionice sunt non-direcțional și nesaturate. Acest din urmă efect este acela că fiecare ion este angajat să aducă la el cea mai mare cantitate de ioni de semn opus, adică să formeze o structură cu un număr mare de coordonare. bond Ionic comune printre compuși anorganici: halogenuri metalice cu sulfuri, oxizi metalici etc. Energia de legare în astfel de cristale este câțiva volți de electroni per atom, deci aceste cristale au o mare rezistență și punct de topire ridicat ..
Noi calcula energia unei legături ionice. Pentru a face acest lucru, ne amintim componentele potențialului energetic al unui cristal ionic:
Coulomb atragerea de ioni de semn opus;
Repulsiei Coulomb de ioni de același semn;
interacțiunea cuantică cu cochilii electronice suprapuse;
van der Waals atracție între ionii.
Contribuția principală la energia de legare a cristalelor ionice face ca energia electrostatică de atracție și repulsie, rolul ultimelor două depozite este neglijabil. Prin urmare, dacă notăm energia de interacțiune dintre ionii și i prin j. energia totală a ionului cu toate interacțiunile sale vor fi
Dăm ca suma potențialelor respingătoare și atractive:
în cazul în care semnul „plus“ este luat ca la fel, și „minus“ - în cazul taxelor opuse. Energia totală a rețelei cristaline ionice, care constă din N molecule (ioni 2N) vor fi
o singură dată ar trebui să fie luate în considerare atunci când se calculează energia totală a fiecărei perechi de ioni cooperat. Pentru comoditate, vom introduce următorul parametru. unde - distanța dintre doi ioni adiacente (încărcate opus) în cristal. astfel
unde constanta Madelung [4] # 945; constante și D sunt definite după cum urmează:
Sumy (2.44) și (2.45) ar trebui să ia în considerare contribuția întregii zăbrele. „Plus“ semn corespunde cu atragerea ionilor opuse, semnul „minus“ - repulsia ioni, cum ar fi.
Constanta este definită după cum urmează. În echilibru, energia totală este minimă. În consecință ,. și, prin urmare, avem
unde - distanța de echilibru dintre ionii învecinate.
iar expresia pentru energia totală a cristalului în starea de echilibru devine
valoare

Ca exemplu, vom calcula constanta de cristal unidimensional Madelung - un lanț nesfârșit de ioni de semn opus care alternează (Fig.2.4).
Fig.2.4. cristal dimensională
Selectarea orice ion, de exemplu, marca „-“ ca initial, va avea doi ioni de semnul „+“ în R0 distanță de ea, două ion marca „-“ în regiunea 2r0, și așa mai departe.
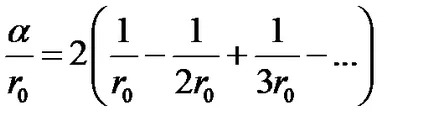
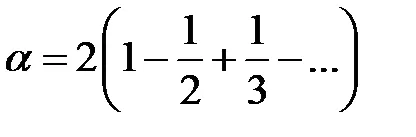
Folosind o serie de expansiune
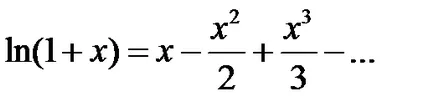
Astfel, expresia pentru energia pe o molecula ia forma
În cazul seriilor de cristal tridimensionale converge condițional, adică rezultatul depinde de metoda de adăugare. Este posibil să se îmbunătățească convergența seriilor, dacă vom izola ionii în rețeaua grupării, astfel încât grupul este electric neutru, și dacă este necesar să se împartă ionul între diferitele grupuri și taxele fracționare administrate (metoda Evjen).
Considerăm că tarifele de pe fețele rețelei cristaline cubice (vezi Figura 2.5) după cum urmează: taxele pe fețele aparțin două celule adiacente (fiecare celulă este de 1/2 din taxa), taxele pe marginile celulelor aparțin patru (1/4 în fiecare celulă), taxe la nodurile aparțin opt celule (1/8 în fiecare celulă). contribuția la # 945; din primul cub poate fi scris ca suma:
Dacă luați următorul cel mai mare cub care include luarea în considerare a noi, obținem. care este de acord bine cu valoarea exactă pentru tipul cu zăbrele. Pentru structurile de tipul obținut. Structura de tip -.
Figura 2.5. Modelul Lattice cu taxe fracționare pentru calcularea unei sume a metodei Madelung Evjen
Să estimăm energia de legare a cristalului. presupunând că parametrul zăbrele, și un modul de elasticitate în cunoscut. Modulul de elasticitate poate fi determinată după cum urmează:
unde - volumul cristalului. Modulul vrac este o măsură de comprimare sub presiune hidrostatică. Pentru cub (fcc) Volumul de tip structură centrată față care este ocupat de moleculele este găzduit
Apoi, putem scrie
Din (2.53) se poate obține cu ușurință derivata a doua
Prima derivată a stării de echilibru este zero, deci de la (2.52-2.54) definesc
Noi folosim (2,43) pentru a obține
De la (2,47), (2,56) și (2.55) vom găsi în vrac modulul B:
Ecuația (2.57) permite calcularea exponentului în potențialul respingător, și folosind valorile experimentale. Pentru un cristal. . . Apoi, de la (2.57) avem
Rețineți că, pentru cele mai multe cristale ionice exponent n în forțele potențiale de repulsie variază între 6-10.
Prin urmare, o valoare mare a gradului de rază scurtă de acțiune provoacă o forță de respingere. Folosind (2.48), vom calcula energia de legare (energie per moleculă)
Acest lucru este de acord bine cu valoarea experimentală a -7.948 eV / moleculă. Trebuie amintit faptul că calculele am luat în considerare numai forțele Coulomb.
Cristale cu covalentă și tipuri ionice de comunicare pot fi considerate limitative cazuri; este un număr între cristale, care au tipuri de conexiuni intermediare. Un astfel parțial ionic () și parțial covalente () legătură poate fi descrisă de funcția de undă
în acest caz, ionicity se determină după cum urmează:
În Tabelul 2.1 prezintă câteva exemple de cristale ale compușilor binari.
Tabelul 2.1. cristale Ionicity