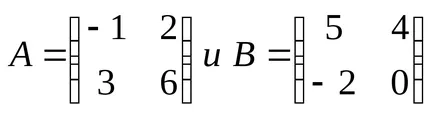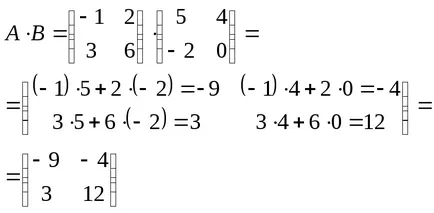Calcularea determinantul de gauss
Calculăm determinant al metodei Gauss.
Metoda constă în următoarele: determinantul reduce la forma triunghiulară, cu ajutorul unor transformări elementare, și dacă este egală cu produsul dintre elementele de pe diagonala principală.
Ideea metodei este următoarea: dat fiind un factor determinant al treilea ordin
element
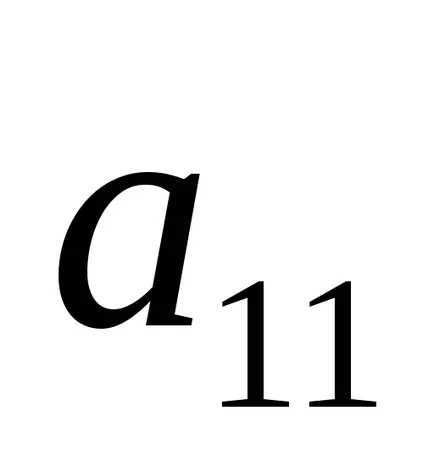
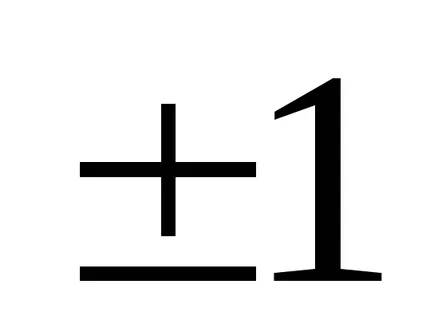
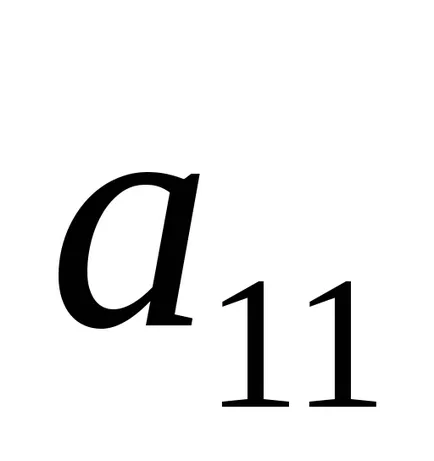
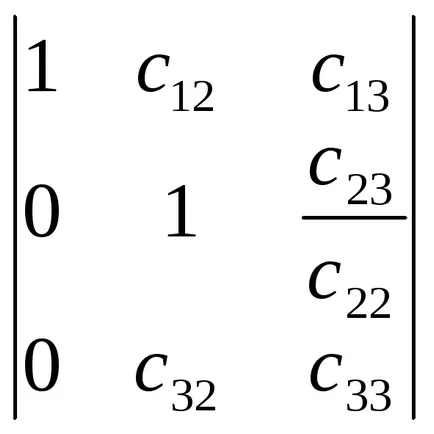
Obținem determinantul formei

Elementele care stau în adus la zero prima coloană, cu excepția primei. Pentru a face acest lucru, mai întâi se scade al doilea rând înmulțit cu
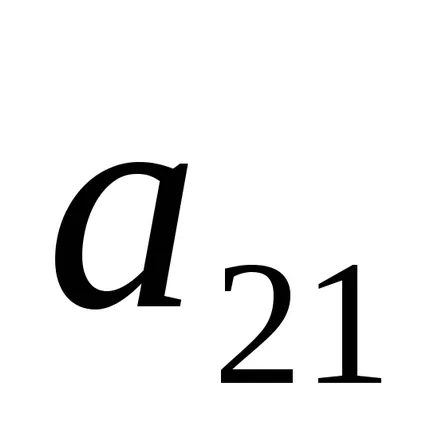

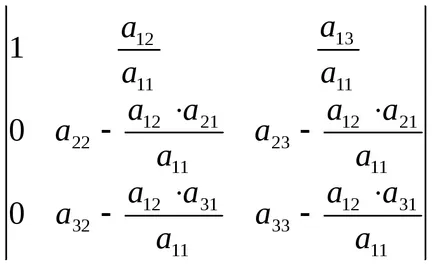
Notăm elementele sale prin litera c, atunci
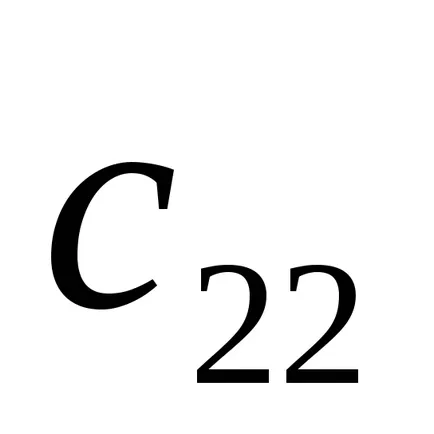
Acum trebuie să resetați elementul

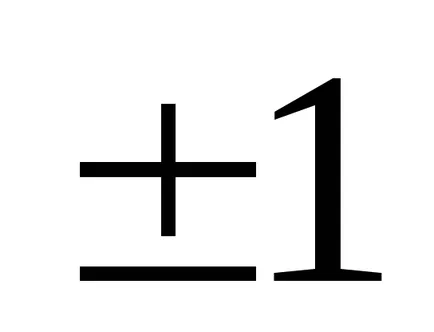
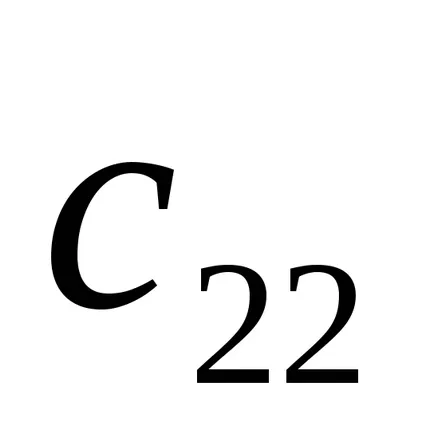
Apoi, un al treilea rând scade al doilea înmulțit cu

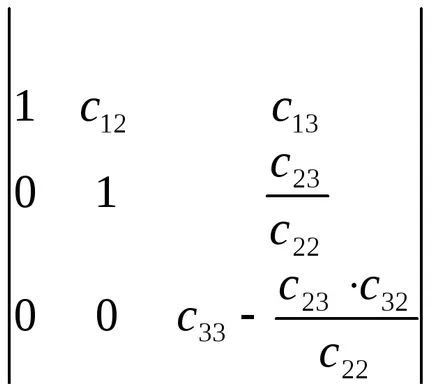
Notăm elementele sale prin litera t, atunci
Aici suntem conduși la determinantul unei forme triunghiulare, acum el este
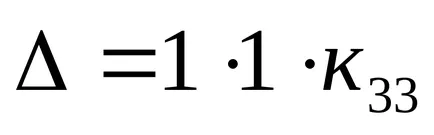
Să examinăm acum acest exemplu specific.
Exemplul 4: Se calculează determinant
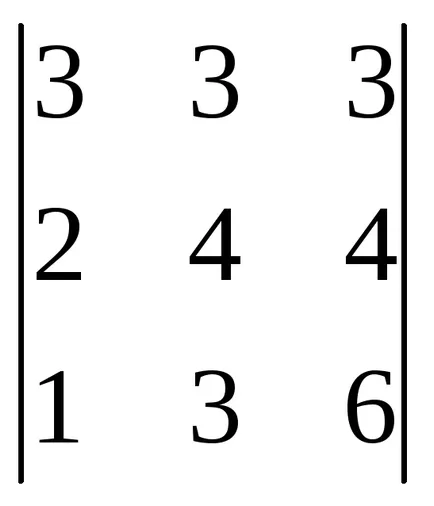
Soluție: interschimbarea primelor și al treilea rând (înlocuirea a două coloane (rânduri) modificări determinante la semnul opus).
scăzând primul din a doua linie, înmulțit cu 2, apoi scade un al treilea rând mai întâi multiplicat cu 3. Ai

Apoi, un al treilea rând scade al doilea înmulțit cu 3.
§2.Matritsy matrici Tipuri
Definiția 7: Dacă matritsemstrok instolbtsov, ea nazyvaetsyarazmernostyu m

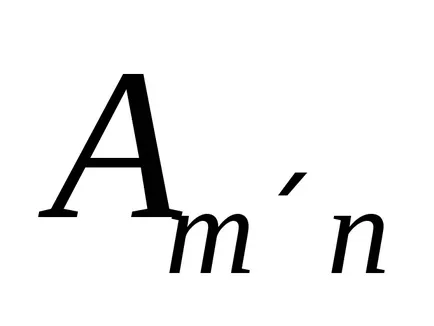
Definiția 8: Dacă
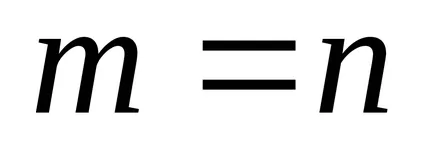
Definiție 9: matrice constând dintr-un singur rând (coloană) se numește matricea-rând (coloană).
10 Definiție: Matricea este format din zerouri, matricea se numește zero.
Definiție 11: Diagonala matrice este o matrice pătrată, în care toate elementele care nu aparțin diagonalei principale sunt zero.
Definiție 12: Matricea de identitate se numește o matrice diagonală, în care toate elementele de pe diagonala principală egal cu unu.
Definiție 13: triunghiulara numita matrice pătrată ale cărei elemente sunt dispuse pe o parte a diagonalei principale sunt egale cu zero.
matrici Deystviyanad.
Definiție 14: Două matrici sunt egale dacă au același număr de rânduri și coloane și egale cu elementele respective.
Matricele A și B sunt egale, adică,
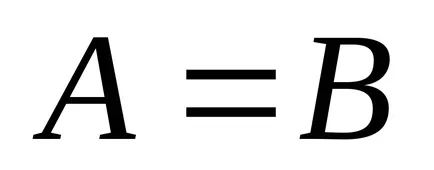
15 Definiție: Suma (diferența) a matricelor A și B este o matrice C, în care fiecare element este egal cu
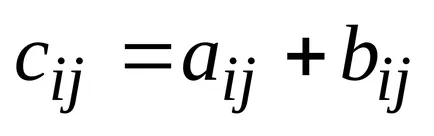
Exemplul 6: Găsiți matricea
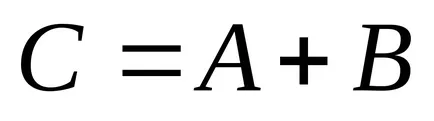
Proprietățile plus
0 2 A + D = A, unde matricea D zero
3 0 A + (B + C) = (A + B) + C (distributiv)
4 0 A + (- A) = O, unde - opusă matricei A
(Adică, elementele au semne opuse)
16: Produsul matricei A de numerele
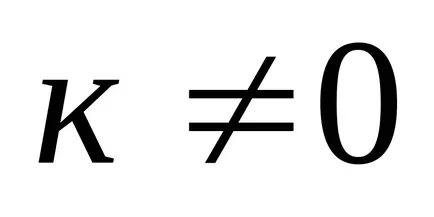

multiplicare Matica
Această acțiune se aplică pentru matricea armonizate așa-numitele.
17 Definiție: Matricea A este coerentă cu matricea B, când numărul de coloane ale matricei A este egal cu numărul de rânduri de V. matricei
Exemplul 8:
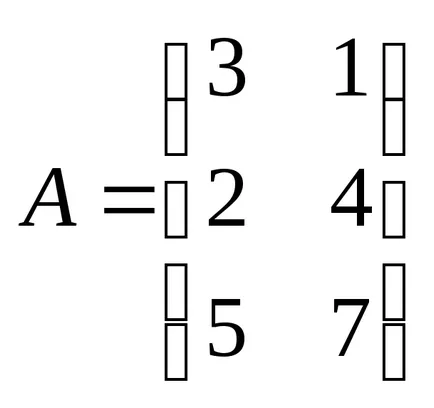
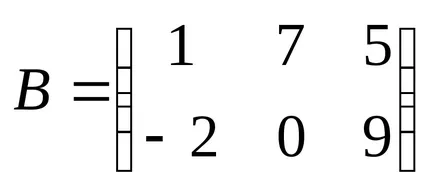
18 Definiție: Produsul a două matrici A și B este o matrice C, unde fiecare element este egal cu suma produselor elementovistroki matricea A care corespunde elementyj-lea coloană a matricei V.
Dacă matricea A are dimensiune
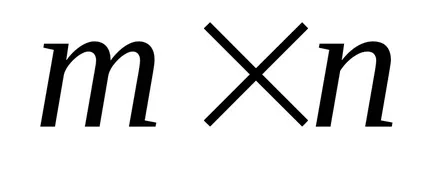
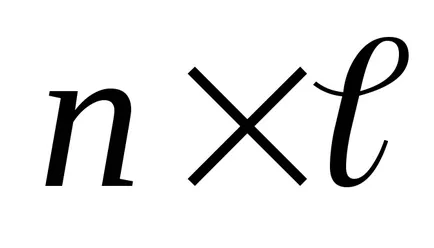
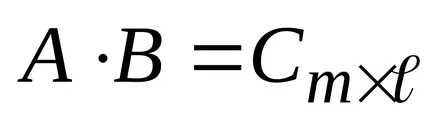
Exemplul 9: Matricea Înmulțire