Bilet la matematică mai mare
Aplicați o substituție simplă în funcție de caracteristicile și tipul integrandul.
1) Când R (-sin x, cos x) = - R (sin x, cos x). raționalizarea cos substituție x = t.
2) Dacă R (sin x, - cos x) = - R (sin x, cos x). raționaliza păcatul de substituție x = t.
3) În cazul în care R (-sin x, - cos x) = R (sin x, cos x). raționalizarea substituția tg x = t. Această substituție se aplică și în cazul integralei este de forma R (tgx) dt
următoarele substituții sunt utilizate atunci când găsirea integralele de tipul:
Sinx = t, în cazul în care n - un număr întreg, număr impar pozitiv
Cosx = t, dacă m - întreg număr impar pozitiv
Tgx = t, în cazul în care m + n - chiar, întreg negativ
Dacă m și n - număr întreg, chiar și numere non-negativ, apoi utilizați formula pentru reducerea ordinului:
Găsirea integralei cele mai simple tipuri de funcții iraționale (în cazul în care a, b, c, d - numere naturale; # 945; # 946; # 947; # 948; - număr natural). Această integrală se reduce la o parte integrantă a unei funktsiis raționale prin substituirea (ax + b) (cx + d) = tk. unde k - cel mai mic multiplu comun # 945; # 946 ;, ..., # 948; # 947;
Proprietățile integrala definită:
Pentru y funcție = f (x). determinată la x = a. egalitate.
Aceasta este, valoarea unei integrala definită cu aceleași limite de integrare egală cu zero. Pentru integrabil pe intervalul [a; b] se realizează funcția.
Cu alte cuvinte, atunci când schimbă limitele superioare și inferioare ale valorii site-uri de integrare a integrala definită este inversată.
4. Un factor constant poate fi luat ca un semn al unei integrale definite. .
6. Dacă funcția y = f (x) este integrabilă pe intervalul [a; b] pentru orice valoare a argumentului, atunci.
8. O valoare medie teorema: c € [a, b],
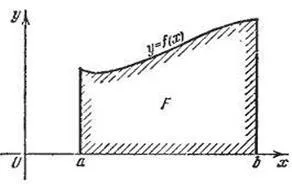
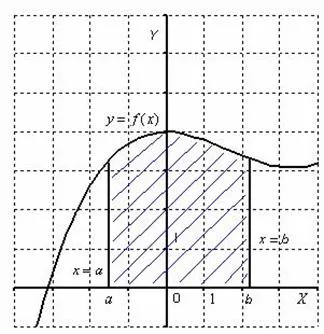
Zona trapezului curbilinie este numeric egal cu definit integralei
Dacă trapez curbată este situată sub axa Ox, S = -
Zona figurii delimitate de curbele y = f (x), y = g (x), astfel încât f (x)<=g(x), находится по формуле:
La calcularea ariei unui trapez curbiliniu, într-un caz în care limita superioară este definită prin ecuațiile parametrice y (t)> = 0, t € [t1, t2], linii drepte x = a, x = b, atunci
(În loc de # 945; și # 946; - t1, t2, în schimb # 966; și un al doilea gunoi - x, y)
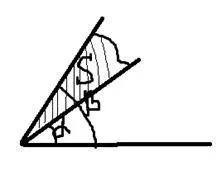
(În loc de p - r)
Dacă trapezoid curbată delimitată de curba x = # 966; (Y) linii drepte y = c, y = d, axa Oy:
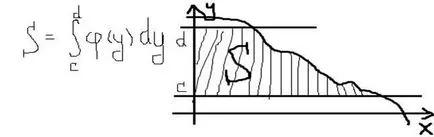
Metode de calcul integralele definite:
Metoda de integrare de către părți: Să intervalul [a; b] sunt definite și funcții continue u (x) și v (x), formula intitulată
Metoda de substituție: Să calculul integralei unei funcții continue de a face substituția x = # 966; (t), t € [t1, t2], dx = # 966; „(t) dt, atunci (în loc de # 945; și # 946; - t1 și t2)
O ecuație diferențială este o ecuație a formei în care - funcția definită într-o regiune a spațiului, - variabilă independentă - o funcție a - derivați ai acestora.
Ordinea ecuației se numește cele mai mari derivați ai ordinelor incluse în ecuație.
Controlați primul ordine: F (x, y, y „), în cazul în care este permisă în ceea ce privește y“, atunci se va arata. t. Pentru a. y '= dydx, dy = y' dx.
dydx = f (x, y); dy = f (x, y) dx
Problema Cauchy pentru primul ordin de sub control: controlul primei comenzi pentru a găsi o soluție care satisface condiția inițială x = x0, y = y0, adică, pentru a găsi curba integrală care trece prin punctul (x0, y0) ...
Soluția generală a ecuațiilor diferențiale ale formei este o funcție y = F (x) + C, determinată în regiunea A, dacă îndeplinește următoarele condiții:
1. Pentru orice valoare a C este o soluție a ecuației F (x, y, y „) = 0
2. Pentru orice condiții inițiale (x0, y0) € D există valori ale C care există y0 ecuație există = F (x0, C)
Soluție de control de sine - orice soluție care se obține din valoarea totală pentru un anumit S.
(M și N se înlocuiește cu P și Q)
Controlul cu mai multe variabile:
- Controlul cu variabile separabile.
Soluție: despartitor de M2 (x) * N1 (y), obținem ecuația
Integrarea, obținem: + - generală integrală
Funcția f (x, y) se numește o funcție omogenă de grad k, în cazul în care identitatea este îndeplinită la toate t. De exemplu, funcția - al doilea grad omogen, care este de a ...
Controlați omogen dacă funcția f (x, y) este o funcție omogenă de ordinul zero.
Controlul uniform adesea stabilit în formă diferențială, unde M și N - funcții omogene de același ordin.
Soluție: O ecuație omogenă este transformată într-o ecuație cu variabile separabile prin substituția: y = u * x, y 'u =' + x „* u, dy = xdu + udx, u = yx
- un control liniar de prim ordin
Proprietăți: necunoscut funcție y și y derivatul său „inclus în ecuația 1 grad nu se multiplica interconectate.
Soluție: Asigurați-vă de înlocuire, în cazul în care - funcția de x.
Din moment ce, atunci, după înlocuirea în ecuația originală, obținem
Gruparea termeni, obținem ecuația
Din ecuație, obținem V și înlocuiți-l.
Să presupunem că, atunci obținem. De aici deducem U .. Să presupunem, atunci funcția - soluția generală
Ecuația diferențială, unde - funcția definită și continuă pe un anumit interval, - ecuația Bernoulli.
Soluție: Asigurați-vă de înlocuire și și să decidă precum și controlul liniar.