11 Tema 11 - site-ul informatikaqw!
Subiect 11 modele optime de planificare
Facilități de planificare poate fi foarte diferit de sistem: activitățile individuale de întreprindere, industrie sau agricultură, ultimul stat din regiune.
Declarația problemei planificării este după cum urmează:
- există unele ținte:. X, Y, și colab;
- Există unele resurse: R1, R2, etc., datorită cărora aceste obiective pot fi atinse .. Aceste resurse sunt aproape întotdeauna limitate;
- există un anumit obiectiv strategic, care depinde de valorile lui X, Y și colab., ținte, care ar trebui să fie orientate de planificare.
Este necesar să se determine valoarea obiectivelor ținând cont de resursele limitate, sub rezerva realizării obiectivelor strategice. Acest lucru va fi cel mai bun plan.
Dă exemple. Lăsați obiectul de planificare este gradinita. Noi ne limităm la cele două cifre țintă: numărul de copii și numărul de cadre didactice. Principalele resurse ale activității grădinițelor sunt finanțarea și suprafața podelei. Care sunt obiectivele strategice? Desigur, una dintre ele este păstrarea și întărirea sănătății copiilor. O măsură cantitativă a acestui obiectiv este acela de a reduce la minimum incidența elevilor de grădiniță.
Un alt exemplu: planificarea activităților economice ale statului. Desigur, este prea dificil pentru noi să-l înțelegem pe deplin. Ținte foarte mult: este producția de diferite tipuri de producție industrială și agricolă, de formare, generarea de energie electrică, mărimea salariilor angajaților din sectorul public, și mai mult. Resursele includ: numărul populației în vârstă de muncă, bugetul de stat, resursele naturale, energia, posibilitatea de a sistemelor de transport și așa mai departe.
După cum vă puteți imagina, fiecare dintre aceste tipuri de resurse este limitat. În plus, cea mai importantă resursă este timpul alocat pentru punerea în aplicare a planului. Problema obiectivelor strategice destul de complicate. Statul are o mulțime de ei, dar în diferite perioade ale istoriei prioritățile obiectivelor pot varia. De exemplu, în timp de război, obiectivul principal este apărarea maximă, puterea militară. Într-un obiectiv prioritar modern, civilizat de stat timp de pace ar trebui să fie pentru a atinge nivelul maxim al populației.
Dacă vrem să utilizați un computer pentru a rezolva problema de planificare optimă, avem nevoie din nou pentru a construi un model matematic. Prin urmare, tot ceea ce a fost spus în exemplele ar trebui să fie traduse în limba de numere, formule, ecuații, și alte mijloace de matematică. În întregime, această sarcină este foarte dificil pentru sistemele reale. Ca și înainte, vom lua calea simplificării. Să considerăm un exemplu foarte simplu, de la care obține o idee de o abordare pentru rezolvarea problemei planificării optime.
Exemplu. Scoala cofetăria pregătește plăcinte și prăjituri. Datorită capacității de stocare limitată pe zi, puteți găti în acest fel nu cumulează mai mult de 700 de bucăți de produse. zi de lucru în magazinul de patiserie durează 8 ore. Deoarece producția de prăjituri mai laborioasă, în cazul în care numai pentru a le elibera, a doua zi se poate face mai mult de 250 de bucăți, chiftelele poate produce, de asemenea, 1000 de piese (în cazul în care nu produce prăjituri). Costul tort este de două ori mai mare decât costul unei plăcintă. Este necesar pentru a face un plan de producție de zi cu zi, pentru a asigura cel mai mare magazin de venituri produse de patiserie.
Desigur, acest lucru este pur și simplu un studiu de caz. Este puțin probabil că există un magazin de patiserie, care produce doar două tipuri de produse, precum și cele mai mari venituri - nu singurul scop al muncii sale. Dar formularea matematică a problemei este simplă. Să rezolvăm.
sunt țintă:
- x - zi plăcinte foaie de parcurs;
- în - prăjituri zi foaie de parcurs.
- durata zilei de lucru - 8 ore;
- Capacitatea de depozitare - 700 locuri de cazare.
Se presupune că pentru simplitate celelalte resurse (materii prime, energie electrică și așa mai departe.) Nu sunt limitate. Formalizarea goluri (maximizând departamentul de venituri) vor fi discutate mai târziu.
Obținerea de relații, următoarele condiții de constrângeri de timp, magazinul de lucru și de depozitare, capacitatea de E. adică. Numărul total de articole.
Din formularea problemei că fabricarea de produse de patiserie petrecut de 4 ori mai mult timp decât o plăcintă de coacere. Notând momentul fabricării ca pateu t min, timpul de producție va fi egală cu tort 41 min. Deci, timpul total de plăcinte și prăjituri producătorului oricum
tx + 4TY = (x 4 + y) t
Dar, de data aceasta nu poate fi mai lungă decât durata zilei de lucru. Rezultă din această inegalitate:
Este ușor să se calculeze T - momentul fabricării de plăcintă. În ceea ce privește timpul de 1000 de bucăți pot fi făcute, atunci pateu petrecut 480/1000 = 0,48 min. Substituind această valoare în inegalitatea, obținem:
(X + 4y) * 0,48 <= 480.
aici
x + 4y <= 1000
Restricții privind numărul total de produse oferă o inegalitate evidentă complet:
Cele două inegalități primite trebuie să adăugați termeni de valori pozitive ale lui x și y (nu poate fi un număr negativ de plăcinte și prăjituri). Ca rezultat, vom obține un sistem de inegalități:
Și acum pentru formalizarea obiectivelor strategice: maximizarea veniturilor. Venituri - este valoarea tuturor produselor vândute. Să presupunem că prețul unei plăcintă - Mr. ruble. Conform declarației problemei, prețul de tort de două ori, adică. F. 2r ruble.
Prin urmare, valoarea tuturor bunurilor produse pe zi este
Rx + 2RY = r (x + 2y)
Scopul de producție este de a maximiza veniturile. Vom lua în considerare expresia scrisă ca funcție de x, y:
Aceasta se numește funcția obiectiv.
Deoarece valoarea lui r - a, valoarea maximă constantă a F (x, y) este atinsă la valoarea maximă (x + 2y). Prin urmare, ca funcție obiectiv poate fi luată
Prin urmare, pentru a obține un plan optim fiert până la următoarea problemă matematică:
Este nevoie de a găsi valori de obiective x și y satisface inegalitățile sistemului și dă valoarea maximă a funcției obiectiv.
Astfel, modelul matematic al planificării optime pentru patiseria școală construit.
Acum, următoarea întrebare este cum să rezolve această problemă?
S-ar putea imagina ca să-l rezolve pentru noi va fi calculatorul folosind un procesor tabel Excel. Și vom discuta doar abordare la o soluție, fără a intra în detaliile metodei.
disciplina matematică, care este dedicat pentru rezolvarea unor astfel de probleme, numit programare matematică. Deoarece funcția obiectiv f (x, y) x și y sunt liniar (m. E. În primul grad), problema noastră se referă la secțiunea acestei științe numită de programare liniară.
Sistemul inegalităților scris mai sus este reprezentat pe un patrulater de coordonate plane delimitată de patru linii drepte ce corespund ecuațiilor liniare:
x + 4y = 1000
x + y = 700,
x = 0 (axa Y),
y = 0 (OSH).
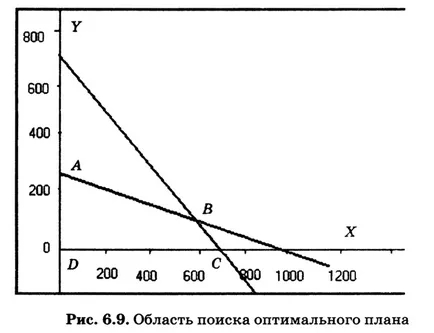
Fig. 6.9 Această zonă este un ABCD patrulater și a subliniat umple. Orice punct al patrulaterului este soluția unui sistem de inegalități.
De exemplu, x = 200, y = 100.
Acest punct corespunde valorii functiei obiectiv f (200, 100) = 400. Un alt punct
(X = 600, y = 50) corespunde f (600, 50) = 700. Dar, evident, soluția dorită este faptul că punctul zona ABCD la care este maximizată funcția obiectiv. Găsirea acest punct este realizată folosind metode de programare liniară.
În Excel arsenalul matematic este o căutare de soluții facilitate. Cum de a rezolva această problemă cu ajutorul acestui instrument, veți învăța de la un atelier de calculator.
Ca urmare a soluționării problemei produce următorul plan optim producția zilnică de magazin de patiserie: este necesar pentru a produce 600 100 plăcinte și prăjituri. Aceste obiective corespund coordonatele punctului B din Fig. 6.9. În acest moment, valoarea funcției obiectiv f (600, 100) = 800. Dacă un pateu este de 5 ruble, venitul rezultat de 4000 ruble.

Întrebări și sarcini:
1. a) Care este problema planificării optime?
b) Care sunt obiectivele, resursele, obiectivul strategic? Dă exemple.
b) Care este programarea matematică, programare liniară?
3. a) Formulați problema planificării optime pentru aer conditionat scoala atelier de lucru în care Terek trei tipuri de produse fabricate: plăcinte, Nye pirozh și biscuiți.
b) Faceți o schimbare în stabilirea planificării optime a acestei probleme secțiuni pentru două tipuri de produse pentru a satisface o altă limitare: numărul de prăjituri nu trebuie să fie mai mic decât numărul de plăcinte. Pe plan de coordonate, vă construi soluția de căutare.