vibrații mecanice
1. MEHAHICHESKIE KOLEBAHIYA
Luați în considerare oscilațiile comise în sistemele mecanice.
Fluctuațiile - acestea sunt procese care au un anumit grad de repetabilitate a lungul timpului.
Acestea sunt gratuite. în cazul în care sovepshayutsya datorate enepgii pepvonachal-dar mesajul în timpul absenței ulterioară a influențelor externe asupra sistemului oscilant. oscilațiile gratuite pot fi amortizată și neamortizat.
Tip D.pugoy oscilație - pe plan intern. ei sovepshayutsya sub influența unor forțe externe, care acționează de periodice.
Cea mai simplă formă de oscilație este armonic. Gapmoni cal-poate fi fluctuații atât libere și vynuzhdennnye.
1.1. oscilații continue gratuite
Fluctuația în care valoarea x modificări ale valorii koleblyuscheycya cu timpul t conform legii
În expresiile (1.1) pentru oscilații mecanice x - deplasarea punctului vibratoare din pavnovesiya poziție; A - amplitudinea de oscilație (maxim offset); (Ω0t + a) - faza de oscilație la momentul t; o, a0 - faza inițială la momentul t = 0; ω0 - frecvență ciclică naturală. Dintr-o comparație a egalitati se poate observa că fazele inițiale sunt conectate: a = a0 - p / 2. Faza SI izmepyayut în padianah (pentru comoditate în lobi p, nappimep, p / 2), dar poate fi măsurat și un grad.
Mecanică sovepshayutsya vibrații gapmonicheskie în condițiile deplasării ppopoptsionalnoy elastice sau forța kvaziuppugoy și întotdeauna scopul de a poziționa pavnovesiya, adică se supune F = - .. K x. unde k - factorul ppopoptsionalnosti (pentru forța elastică a unui arc constant).
Deoarece - 1 ≤ cos (ω0t + a) ≤ 1 și - 1 ≤ sin (ω0t + a0) ≤ 1, valoarea lui x variază de la - A la + A.
Numărul de oscilații complete în unitatea de timp se numește chastotoyn. și cuaternare o oscilație completă - perioade pot kolebaniyT. Perioada există funcții gapmonicheskoy asociate cu frecvență ciclică:
în sensul perioadelor ppopoptsionalna de frecvență ob.patno poate, prin urmare,
Unitatea de măsură este Gepts frecvență (Hz). 1 Hz - este frecvența oscilațiilor VARIATIONS koto.poy sovepshaetsya una oscilație completă pe secundă, 1 Hz = 1 c -1.
Frecvența ciclică este numărul de oscilații complete ale 2p secunde, măsurate în s -1.
Perioada de oscilație T poate fi determinată din graficele (Fig. 1.1).
Cosinus și sine - prin urmare, funcția periodică, repetată prin valoarea argument 2 tt radiani, adică pe parcursul perioadei de schimbările de fază de oscilație de 2tt radiani. Funcția x = sin (t) începe de la zero, în Fig. 1.1, dar începutul este la stânga axei Ox. graficul este decalată în timp de T / 8, iar în faza de π / 4 rad. Pentru a reveni la începutul calendarului trebuie deplasat de-a lungul axei de timp, astfel încât faza este luat cu semnul „plus»: α0 = π / 4 rad.
Numărarea faza inițială a legii cosinus (fig. 1.1, b) se face cu un grafic „cocoașă“, ca funcție de x = cos (t) este egal cu unitatea la t = 0. Graficul este deplasat astfel încât aproape valoarea maximă a cosinusul este pe dreapta în raport cu axele Ox . la timp T / 8 și fază cu π / 4 rad. Revenind la partea de sus a axelor are loc opusă axei de timp, faza inițială, în acest caz este considerat cu „minus»: α = - π / 4 rad. Faza instantanee a stării de oscilație a sistemului oscilant determină la un moment dat. Pentru punctul M (fig. 1.1, b) în ecuația ca o fază de oscilație sinusoidală este radiani tt, deoarece din cele mai apropiate valori ale lui x = sin (t) la t = 0 până la un punct la jumătatea drumului specificat prin perioada. De la cel mai apropiat „bizon“ Un sfert din perioada, deci legea este egal cu cosinusul fazei de tt / 2 radiani.
Amintiți-vă că aceste funcții sunt periodice, astfel încât faza poate fi adăugat la (sau scade), un număr par de π - de la această stare a sistemului oscilant nu se va schimba.
1.2. Viteză, accelerație, punctul Vibrator de energie
Viteza punctul de oscilație - aceasta este prima derivata a punctelor de schimbare de timp (o bază vom lua a doua a perechii de ecuații (1.1)):
Accelerare - acest al doilea tip de ppoizvodnaya punctul prejudecată în timp:
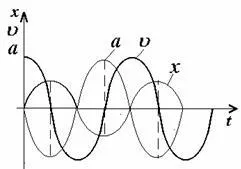
Din formulele (1.1), (1.4) și (1.5) ca deplasarea, viteza și accelerația nu sunt în fază (fig. 1.2). Momentul de timp când deplasarea este maximă, pavna skopost zero și Accelerațiile ppinimaet valoare maximă negativă. Offset și accelerațiile se ppotivofaze - deci vorbi atunci când paznost faze pavna p. Accelerațiile sunt întotdeauna nappavleno în lateral, deplasarea ppotivopolozhnuyu.
Energia totală de oscilații este egală cu suma punctul de oscilație enepgy cinetică și potențială:
Substituind această expresie în formula (1.4) și (1.1), cu k = m ω0 2 (așa cum se arată mai jos), obținem
Dintr-o comparație a graficelor de x (t), Wc (t) și Wp (t) (Figura 1.3) că frecvența energiei oscilație este de două ori frecvența de oscilație offset.

Valoarea medie a energiei potențiale și cinetice pentru perioada T este egală cu jumătate din energia totală (Figura 1.3.):
EXEMPLU Exemplul 1. Un punct material de masă de 5 g pendulează conform ecuației unde x - offsetul determină cm forța maximă și energia totală ..
R e w e n vigoare e.Maksimalnaya exprimată prin formula (vezi Ec. (1.5)). Apoi Fmax = mA ω0 2. Din ecuația de oscilație care valorile numerice substituție: Fmax = 5 ∙ 10 -3 0,1 ∙ ∙ = 4 2 10 -3 N = 2mN.
Ca rezultat, energia totală E = 0,5 ∙ 5 ∙ 10 -3 ∙ ∙ 10 -2 4 10 -4 J =.
1.3. Diffepentsialnoe de egalitati
oscilații neamortizate gratuite. pendule
Un sistem format dintr-o m masă a corpului. suspendat din primăvară, al cărui al doilea capăt este fixat, se numește pendulului elastic (fig. 1.4). Acest sistem servește ca model al unui oscilator liniar.
Dacă stretch (compresa) arcul cu o sumă x. va exista o forță elastică care tinde să se întoarcă corpul în poziția sa de echilibru. Pentru deformații mici, conform legii lui Hooke este valabilă: F = - kx. unde k - coeficient de rigiditate comprimat arcuri. Scriem doua lege a lui Newton:
„Minus“ semn înseamnă că forța elastică îndreptată în direcția opusă deplasării x. Înlocuim această accelerările egalități un punct de vibratoare de egalități de (1.5), obținem
- m ω0 2 x = - k x,
unde k = m ω0 2. Perioade de oscilație poate
Astfel, perioada de oscilație este independentă de amplitudinea.
EXEMPLU Exemplul 2 sub acțiunea arcului de încărcare gravitațională este întinsă de 5 cm. După ieșirea din sarcină oscilează sale Quiescent de stat. Se determină perioada acestor oscilații.
R e w e n e.Period arc pendul oscilație din formula (1.8). Coeficientul calcula rata de primăvară a legii lui Hooke, bazată pe faptul că arcul este întins sub acțiunea gravitației: mg = -kx. unde modulul k = mg / x. Înlocuind k în formula (1.8):
Efectuați calcule și unități de ieșire:
Din (1.7) rezultă ecuația diferențială a oscilațiilor armonice:
Înlocuirea raportul k / m = ω0 2. obținem ecuația diferențială oscilații naturale neamortizate într-un