Studiu de design și funcția plotare
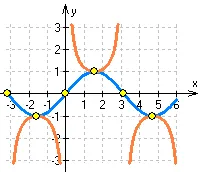
testele funcționale (folosind instrumente derivate) - loc de muncă pe scară largă în cursul școlare și universitare de matematică, care vă permite să verificați cunoștințele și abilitățile în mai multe ramuri ale matematicii (informații generale despre funcțiile, funcțiile de conversie, limitele, derivate și aplicațiile sale).
Scopul cercetării este de a studia funcția de proprietăți importante ale funcției și construcția graficului rezultatelor (care este motivul pentru care, uneori, sarcina este formulată ca un „studiu al graficului“). Pentru a desena un grafic în mod corespunzător, trebuie să efectuați în mod consecvent etapele studiului.
Conducerea o funcție completă de investigare
Mai jos este un plin circuit de test funcție (sau teste ale funcției algoritm) punct cu punct. Unele dintre aceste etape sunt de obicei omise atunci când studiul funcției, în funcție de tipul de cerințe funcționale și la soluția (de exemplu, polinomul nu poate verifica asymptotes sau puncte de discontinuitate etc.).
Puncte cheie (design de studiu de bază) sunt marcate cu negru, elemente care sunt incluse în studiu opționale sunt evidențiate cu gri.
- Găsiți domeniul funcției.
- Găsiți intervalul funcției. De obicei, acest punct este trecut sau completat, după cercetări pe extreme.
- Pentru a investiga functia de continuitate, de a aloca punct specific (punct de discontinuitate).
- Verificați până asymptotes verticale în punctele de discontinuitate în limitele și definiția de suprafață.
- Găsiți punctul de intersecție cu axele de coordonate.
- Găsiți zerouri. Găsiți intervalele ale funcției semn constantă.
- Stabiliți dacă funcția este par sau impar. Pentru a trage concluzii cu privire la simetria graficului funcției.
- Pentru a stabili dacă este sau nu o funcție periodică. De obicei, verificați pentru funcțiile trigonometrice, pentru alții este omis acest element.
- Găsiți primul derivat. Găsiți extremum punctul (local maxim și minim) și intervalele de monotonie (creșterea și descreșterea) funcție.
- Găsiți derivata a doua. Găsiți un punct de inflexiune, și intervale de convexitate-concavitate.
- Găsiți funcția asimptotă înclinată / orizontal.
- Pentru a investiga comportarea funcției la infinit.
- Construi un grafic al funcției. Build asimptotă.
- Mark puncte importante pe grafic.
Utilizați acest algoritm pentru a rezolva sarcinile lor pentru studiul funcțiilor și vă dobtes succes. Avem nevoie de mai multe exemple pentru a înțelege „pe degete“? Pe site-ul veți găsi exemple de funcții de cercetare de diferite tipuri, pe care le puteți descărca gratuit pentru a explora.