Structura unui circuit electric
Proprietățile structurale sau topologice includ circuite astfel caracteristicile sale, care nu sunt legate de caracteristicile elementelor sale constitutive active și pasive. Acestea includ următoarele concepte: un circuit de nod ramură.
porțiune de circuit de ramură se numește, ale cărui elemente sunt conectate în serie unul în spatele celuilalt și sunt raționalizate de același curent.
Circuit de nod numit o joncțiune a mai multor ramuri. Nodul se leagă de cel puțin trei ramuri și un punct de ramură.
Ramurile sunt considerate conectate în serie în cazul în care acestea sunt raționalizate de același curent. Ramurile sunt considerate conectate în paralel, în cazul în care acestea sunt conectate la aceeași pereche de noduri. Astfel, o conexiune serie de elemente pentru parametrul lor comun este curent în paralel - tensiunea între noduri.
o buclă de circuit electric este un set de ramuri consecutive. Nodurile în care sunt conectate aceste ramuri, sunt punctele de ramificare. Atunci când traversează o buclă închisă și începe puncte finale coincid. În continuare înțeles de către circuitul de buclă închisă.
Lanț în care nu ramificare sunt numite singur, în prezența branșamente - multiloop. Circuit buclă multiplă caracterizată prin numărul de bucle independente. Setul de circuite independente este determinată de faptul că fiecare dintre buclele ulterioare, pornind de la elementar, caracterizat prin cel puțin o ramură nouă. Numărul de circuite independente pot fi determinate prin formula lui Euler:
în cazul în care m - numărul de sucursale,
n - numărul de noduri, în care m> n ori.
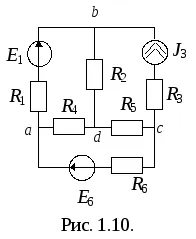
Circuitul din Fig. 1.10. patru noduri: a, b, c, d; șase ramuri: ab, bd, BC, anunțuri, DC, AC. astfel numărul de căi independente este determinat prin formula Euler, după cum urmează:
Aceasta poate include următoarele circuite: ABCD, DBC, sau Abd adc, DBCA, adc și altele.
Legile lui Kirchhoff
Legile lui Kirchhoff sunt baza teoriei lanțurilor liniare și sunt la fel de legea lui Ohm, o generalizare a datelor experimentale.
Izakon Kirchhoff (pentru curenți). suma algebrică a curenților de la nodul este egal cu zero, sau valoarea și cantitatea ce se scurge jetul de umplere a curenților la fel. Ca o regulă, însumarea curenților inflowing sunt preluate din semnul „+“, și care expiră - cu semnul „-“.
IIzakon Kirchhoff (pentru stres): suma algebrică a tuturor surselor CEM întâlnite atunci când traversează conturului, egală cu suma algebrică a tensiunilor la toți consumatorii. În formă algebrică
In concluzie, cu semnul „+“ include EMF contribuie surse (adică surse care sunt într-o direcție concordantă cu circuitul de by-pass) și cu semnul „-“ surse EMF opuse. În însumarea tensiuni consumatorilor cu semnul „+“ este luată pentru toți consumatorii de tensiune, din care curenții sunt direcționate în conformitate cu circuitul de by-pass, și semnul „-“ tensiune este luat de toți ceilalți utilizatori. Direcția buclă parcurgeri este selectată în mod arbitrar.
Conversia circuitelor electrice pasive liniare
Porțiunea de conversie echivalentă circuitului pasiv este un înlocuitor al lanțului său alt pasiv, în care rămân curenții constante și tensiuni de repaus a circuitului nu este supus transformării. Prin transformări simple, includ înlocuirea serii și consumatori conectat în paralel echivalent pentru consumator.
Într-o conexiune serie rolul de rezistență echivalentă (sau consumator echivalent rezistență) joacă o sumă a rezistenței tuturor consumatorilor (Fig. 1.11.).
(1.10) Rezultă din Legea II Kirchhoff:
Atunci când doi consumatori conectat seria de:
În legătură paralelă rolul conductibilitate echivalentă (sau consumator echivalent conductibilitate) joacă suma conductivitățile tuturor consumatorilor (Fig. 1.12.).
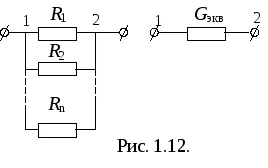
Din legea lui Kirchhoff I:
Atunci când cei doi consumatori legate în paralel, de:
Astfel, pentru un circuit de calcul cu consumatorii din seria oportun să-și exprime proprietățile lor de valori ale rezistenței și conectate în paralel - valorile conductivitățile.
Determinarea rezistenței echivalente din compusul mixt de consumatori se realizează prin simplificarea treptată (pliere) a circuitului original.
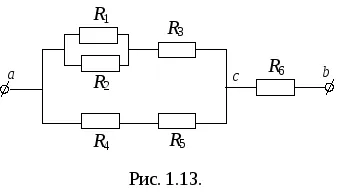
Seria de conectare R12 și R3:
conexiuni de R4 și R5:
Conectarea în paralel cu R123 și R45.
RAC conexiune Series și R6:
Astfel, rezistența echivalentă
Mai complicat este conversia reciprocă a consumatorilor racordați stea sau triunghi. Astfel de transformări ar trebui să fie manipulate în acele cazuri în care conexiunea să fie de simplificare, este imposibil să se aloce o paralelă sau conexiuni seriale consumatori.
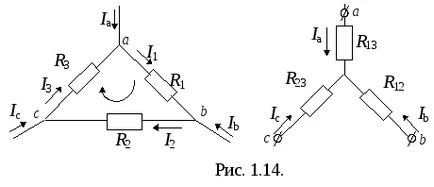
Nodurile a. b. c și triunghiul. și stea în Fig. 1.14. conectat la restul circuitului. Conversia triunghiului în steaua trebuie să fie de așa natură încât aceleași valori ale potențialului de puncte ca un triunghi și stele curg la aceste puncte, curenții au fost egale, atunci toate circuit extern „nu va observa“ înlocuire produs.
Uab exprimă triunghiul prin opțiunile de consumatori și care curge la aceste noduri curenți. Noi scriem ecuațiile lui Kirchhoff pentru un circuit și nodurile și b.
Înlocuiți în prima ecuație a I3 curenților și l2 în expresiile corespunzătoare:
Conform legii de tensiune Uab lui Ohm pentru conectarea consumatorilor triunghi:
Acum avem o expresie pentru aceeași tensiune în legătură stea consumatorilor:
Pentru circuitele de date de echivalență la valori arbitrare ale curenților Ia și Ib este necesară egalitatea de tensiuni Uab pentru conectarea consumatorilor delta și stele. Acest lucru este posibil doar în aceiași coeficienți de ecuații (1.15) și (1.16), adică
În mod similar, putem obține o expresie pentru a determina:
Astfel, rezistența stelei fasciculului este produsul de rezistență laturile adiacente ale triunghiului împărțit la suma rezistenței triunghiului trei laturi.
Formula inversă transformare poate fi derivat în mod independent sau ca o consecință a (1,17) și (1,18) prin conducția:
sau prin rezistența:
Prin urmare, o parte a rezistentei triunghiului este egală cu suma rezistențelor punctelor adiacente ale stelei, iar lucrările lor sunt împărțite de rezistența celui de al treilea fascicul.