Semne ale funcțiilor trigonometrice - studopediya
Funcția de conectare trigonometrice depinde exclusiv de trimestru coordonate, care este un argument numeric. Ultima dată când am învățat să traducă argumentele măsurii Radian în grade (vezi. Lecția „măsură Radian și gradul unghiului“), iar apoi determina trimestru cele mai coordonate. Acum vom, de fapt, definiția sine plăcii, cosinusul și tangenta.
sinusul unghiului # 945; - o coordonată (coordonata y) punct pe cercul trigonometric, care apare la rotirea razei printr-un unghi # 945; .
cosinusul unghiului # 945; - este abscisa (coordonate x) punct pe cercul trigonometric, care apare la rotirea razei printr-un unghi # 945; .
Tangenta unghiului # 945; - raportul dintre sinusul la cosinusul. Sau ce este același lucru, raportul dintre y-coordonate la coordonate x.
Toate aceste definiții sunt familiare pentru tine de la curs de algebra de liceu. Cu toate acestea, suntem interesați nu o definiție proprie, precum și consecințele care apar pe cercul trigonometrice. Aruncati o privire:
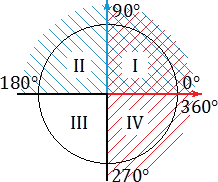
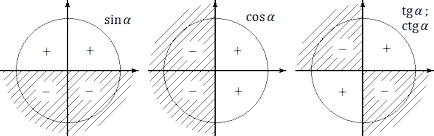
Culoarea albastră a indicat o direcție pozitivă OY axe (axa ordonată), roșu - axa pozitivă direcția OX (abscisă). În acest „radar“ semne devin funcții trigonometrice aparente. În special:
1. păcat 945 #> 0, dacă unghiul # 945; Acesta se află în I sau II de coordonate trimestru. Se proiskhoditiz faptul că, prin definiție, sinus - este abscisa (coordonate y). O coordonată y este pozitivă coordonate cu precizie I și II sferturi;
2. cos 945 #> 0, dacă unghiul # 945; Acesta se află în I sau IV coordonate trimestru. Deoarece numai tamkoordinata x (alias - abscisa) este mai mare decât zero;
3. tg 945 #> 0, dacă unghiul # 945; este I sau III, în trimestrul de coordonate. Rezultă din definiția: pentru tg # 945; = Y. x. deci este pozitivă numai în cazul în care x și y sunt aceleași semne. Acest lucru are loc în I trimestru coordonate (unde x> 0, y> 0) și coordonate trimestru III (x <0, y <0).
Pentru claritate, observăm semne ale fiecărei funcții trigonometrice - sinus, cosinus și tangente - în unele „radar“. Obținem următoarea imagine: