Proprietățile de bază ale seriei de putere - studopediya

1) În toate punctele situate în intervalul de convergență, valoarea seriilor de putere este o funcție continuă a variabilei x:

2) Termenul serie de puteri de termen pot fi integrate în intervalul de convergență:

3) termenul serie de putere prin termenul se poate diferenția intervalul de convergență în interiorul:

Când termwise integrarea și diferențierea seriei de puteri de intervale de convergență nu se schimbă.

Exemplul 4. Găsiți suma seriei

Decizie. Mai întâi vom găsi intervalul de convergență a seriei N

În consecință, un număr de interval de convergență (-1, +1). Diferențierea (3.6), avem

S ¢ (x) = 1 + x 2 +. + X n +.

Partea dreaptă a acestei expresii - seria geometrică cu q = x, convergent pentru ½x½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим

Prin urmare, suma seriei originale vor găsi integrare

Găsim C. Din (5.6) rezultă că S (0) = 0. Prin urmare,

0 = - ln (1-0) + C, C = 0.

Prin urmare, S (x) = - ln (1-x) =.

Împreună cu seria de putere în raport cu variabila x este adesea considerată seria de putere variabilă (x-a), adică, serii de forma:

Evident, acest număr prin substituirea y = (x - a) este convertit într-o serie de tip (3.3). Prin urmare, în cazul în care seria de putere (3.3) este intervalul de convergență - R

serie Taylor. Să presupunem că funcția f (x) x = o are derivați de orice ordine. Să presupunem că există o serie de puteri convergente

a0 + a1 (x-a) + a2 (x-a) 2 +. AN + (x-a) n +. = (3.8)

valoarea care este egală cu funcția f (x). și anume

Coeficienții din această serie. Evident, f (a) = a0. Diferențierea (3.8) la x = a. au a1 = f ¢ (a). Diferențierea (3.8) la x = dublu obține a2 = (f ¢¢ (a)) / 2. Continuând derivarea (3.8), putem observa că un număr de factori (sunt în conformitate cu formula

Puterea serie de forma

Funcția nazyvaetsyaryadom Taylor f (x).

În cazul particular a = 0 este dată de o serie Taylor

și se numește seria Maclaurin.

Exemplul 5 într-o funcție Taylor serie f (x) = e x.

Decizie. Deoarece e x = (e x) ¢ = (e x) = ¢¢. (E x) n. apoi la x = 0 pentru f (x) = e x au

f (0) = 1; f ¢ (0) = 1; f ¢¢ (0) = 1;. ; f (n) (0) = 1;.

Prin urmare, funcția Maclaurin y = e x are forma

Series (3.11) converge pe întreaga axă la funcția y = e x.

Exemplul 6. Descompune funcția Maclaurin f (x) = sinx.

Decizie. Pentru funcția f (x) = sin x, avem: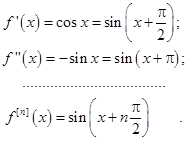

Prin urmare, seria Maclaurin pentru sin x:

In mod similar, obținem o expansiune pentru cos funcția x:

În mod similar, puteți obține o serie de expansiune Taylor sau Maklorenai multe alte funcții.