proiecție în perspectivă

Metoda de proiecție axonometrică este că figura cu axele de coordonate rectangulare, la care este alocată în spațiul este proiectat în paralel pe un plan, adoptat pentru proiecție axonometrică plane 1 (acest plan este numit, de asemenea, planul imaginii).

1 Axonometry - din greacă "Axon" - axa "metru" - măsurat.

Când proiecția paralelă atunci când direcția de proiecție perpendiculară pe proiecția plană axonometrică, vedere în perspectivă a unui apel dreptunghiular; în cazul în care direcția de proiecție este perpendiculară pe planul de proiecție, vedere în perspectivă oblică a unui apel. Utilizat în proiecție axonometrică internă documentația de construcție standardizată GOST 2.317-69.

Luați în considerare formarea de proiecții axonometrice pe exemplu imaginea unui paralelipiped cu baza pătrată (fig. 6.1), prin transformarea secvențială proiecția ortogonală cu axe. Prin rotirea paralelipipedului (a) cu axele x și y în jurul axei z conform săgeții A de 45 ° obține imaginea (b) cu axele rotite x1 și y1 conservate și axa verticală z. Prin activarea proiecției de imagine profil cu axele z, x1. y1 săgeții B printr-un unghi de 30 ° se obține o imagine (c) cu axele z1. x2. y2 situat la anumite unghiuri ale tt plane (π ' „). proiecție paralelă (g) de săgeată în planul L este o vedere axonometrică a casetei cu axele pi plan. un plan de perspectivă nu este desemnată (este planul hârtiei).

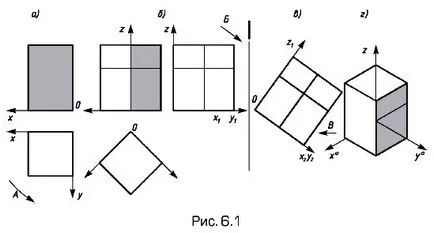
Proiecțiile axele x y 0. 0 0. z proiecții plane axonometrice numite axe axonometrice (denumite în continuare „0“ indicele va fi omisă).

Atunci când aranjament reciproc diferită a axelor în spațiu și planul de proiecție axonometrică și la diferite direcții de proiecție pot fi setate pentru a primi proiecții axonometrice diferite de direcție axe axonometrice și solzi pe acesta. Această poziție a demonstrat Teorema K. Polke. Luați în considerare unele dintre ele.

coeficienții de distorsiune

Fig. 6.2 prezintă un sistem spațial de coordonate ortogonale Ox, Oy, Oz, segmente individuale e pe coordonate și axele lor de proiecție în direcția s pe un plan π, care este planul de proiecție axonometrică. Proiecția ex. ey. ez segment e axonometrică axe la respectiv 0 ° x °, O ° y °, O ° z ° este, în general nu este egal cu segmentul și e nu sunt egale între ele. segmente Ex. ey. ez sunt unitățile unei perspective axelor - unități axonometrică (scala axonometrie).

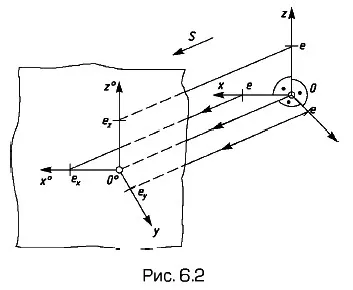
numit coeficienții unei axe distorsionării perspectivei.

În cazul particular al poziției planului de imagine poate fi aleasă astfel încât unitățile axonometrice - segmente de ex. ey. EZ - toate sunt egale între ele sau să fie egale între ele o pereche de aceste segmente.

Când Ex = ey = ez (k = m = n) se numește o vedere în perspectivă izometrică; distorsiuni pe toate axele în ea sunt aceleași. La egalitate axonometrice biaxial unități, în mod tipic la ex = ez ≠ ey (k = n ≠ m), avem proiecție dimetric. Dacă ex = EY ≠ EZ. proiecția numită trimetrică.

tt planul de imagine din Fig. 6.3 este prezentat astfel încât acesta intersectează cele trei axe de coordonate Ox, Oy, Oz la punctele x, y, z respectiv. Luați în considerare o perspectivă dreptunghiulară. În acest caz, TOE segment ° π plan perpendicular. Întind ° O x, y O °, O ° z este o vedere axonometrică a segmentelor Ox, Oy, Oz și picioarele sunt triunghiuri dreptunghiulare ipotenuza care - segmentele Ox, Oy, Oz. Notăm unghiurile dintre axele de coordonate și proiecțiile lor pe planul tt prin α, β, y.

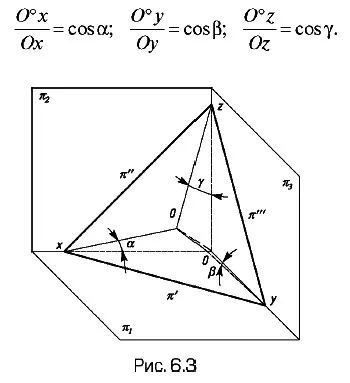
Aceste relații sunt coeficienții de distorsiune, adică,

k = cos alfa; m = cos β; n = cos γ.

Este cunoscut faptul că pentru un segment OO ° ⊥ suma π a pătratelor cosinusului direcție este egal cu unu:

păcatul 2 α + sin 2 β + sin 2 γ = 1

1 - cos 2 +1 alfa - cos 2 β +1 - cos 2 γ = 1.

cos 2 α + cos 2 p + cos 2 γ = 2

k 2 + m 2 + 2 = 2,