programare liniară
x1. x2. xn - variabile de intrare, xn + 1. xn + 2. xn + m - variabile suplimentare. Toate variabilele suplimentare care le-am luat ca bază. și variabile care încep nonbasic (înregistrate în continuare în prima coloană a tabelului și simplex începând din primul rând). La fiecare iterație a elementelor de masă simplex recalculate în conformitate cu anumite reguli.
Algoritmul metoda Simplex.
Aici este problema LP la forma canonică
În cazul în care problema inițială trebuie să se găsească cel puțin - semnele coeficienților funcției obiectiv F sunt inversate A0, n = -a0, n. Semne de constrângeri coeficienții de semnul „≥“ doar inversat. În cazul în care starea conține semnul „≤“ - coeficienții sunt scrise neschimbate.
Etapa 0. Formăm tablou simplex care corespunde problemei inițiale
Pasul 1. Se verifică valabilitatea.
Verificați pe elementele pozitive ale coloanei b (termeni constante), în cazul în care nici unul dintre ele este negativ, atunci am găsit o soluție fezabilă (o soluție care corespunde uneia dintre vârfurile condițiilor poliedru) și trece la pasul 2. Dacă există elemente negative în coloana membrilor de a alege între ei maxim modulul - setează lider șirul k. Această linie găsi, de asemenea, elementul de maxim modul negativ ak, l - stabilește coloana de conducere - l și este un membru de frunte. Variabila corespunzătoare rândului de conducere este exclus din baza, variabila corespunzătoare este inclusă în baza de conducere coloană. Recalcula tabelul simplex în conformitate cu normele.
Dacă există elemente negative în rândul membrilor liberi - și în rândul corespunzător - nu există condiții ale problemei sunt inconsistente, și nu are soluții.
În cazul în care, după recalculare membrilor libere ale coloanei au rămas otritsaetelnye elemente, vom trece la primul pas, în cazul în care nu există nici una, apoi a doua.
Pasul 2: Verificați pentru optimalitate.
La etapa anterioară am găsit o soluție fezabilă. Verificați-l pentru optimalitate Dacă printre elementele nahodschihsya tabelul simplex în rândul F (fără a lua în considerare elementul B0 - valoarea curentă a funcției obiectiv) nu este negativ, atunci am găsit soluția optimă.
În cazul în care linia F, există elemente negative ale soluției trebuie să fie îmbunătățită. Alegerea între elementele negative ale liniei F a modulului maxim (excluzând valoarea funcției B0)
l - o coloană în care el este de a fi lider. În scopul de a găsi o linie de plumb, găsi raportul membrului respectiv liber și membru al coloanei de conducere, cu condiția ca acestea să fie non-negativ.
k - rândurile pentru care acest raport este minim - lider. Element ak, l - prezentator (autorizare). Variabilă corespunzător liniei de conducere (xk) este exclus din baza variabilei corespunzătoare coloanei de conducere (xl) este inclusă în baza.
Recalculăm formulele tabel simplex. În cazul în care elementele negative rămân în noul tabel de alocare, după un rând F mergeți la pasul 2
Dacă nu puteți găsi o linie de plumb, deoarece nu există elemente pozitive în coloana de lider în domeniul soluțiilor fezabile ale caracteristicii problemă nu se limitează la - algoritmul se oprește.
Dacă linia F din coloana membrilor tuturor elementelor sunt pozitive, atunci am găsit soluția optimă.
reguli de transformare simplex de masă.
La elaborarea noului tabel simplex în ea apar următoarele modificări:
- În schimb, baza XK variabila a scrie xl; în locul variabilelor nonbasic xl scrie XK.
- elementul de conducere se înlocuiește cu reciproca ak, l „= 1 / ak, l
- toate elementele care conduc pe coloană (cu excepția ak, l) înmulțit cu -1 / ak, l
- toate elementele rând de conducere (cu excepția ak, l) înmulțită cu 1 / ak, l
- Elementele rămase masă simplex sunt convertite din formula ai, j „= ai, j - ai, l x ak, j / ak, l
Elemente de conversie Schema tabel simplex (cu excepția rândului de conducere și plumb coloană) schemă numită „dreptunghi“.
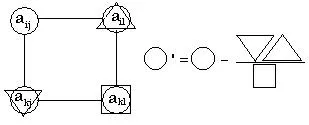
Element decapotabil ai, j și cei trei factori corespunzători sunt doar vârful „dreptunghi“.