Prism și o cutie
Face din cutie, fără noduri comune sunt numite opuse. [4, 301]
Paralelipiped ale cărei margini laterale sunt perpendiculare pe planul de bază, numită paralelipipedului directă. El are toate fețele laterale ale bazei dreptunghiuri și paralelogram. Dacă toată fața caseta - dreptunghi, este numit un paralelipiped dreptunghic. Lungimile trei dintre margini, care se extind de la un nod, numit dimensiunile unui paralelipiped dreptunghiular.
Paralelipiped toate cele trei dimensiuni sunt egale se numește un cub. Raportul dintre diferitele tipuri de paralelipiped prezentate în următoarea schemă: [2, 115]
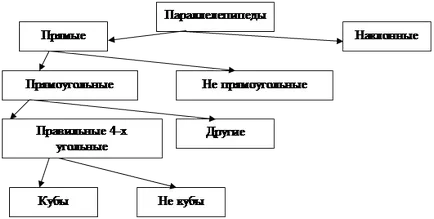
1) și fețele opuse sunt paralele;
2) toate cele patru diagonale se intersectează la un moment dat și împărțiți-l în jumătate.
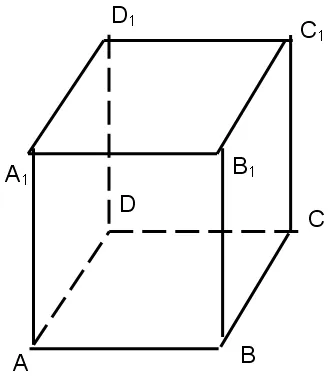
1) Luați în considerare oricare două fețe opuse ale cutiei, de exemplu,
Dimensiune cub: D = a√3.
Perimetrul bazei: P = 4a.
2. Linia de bază a prismei este un triunghi isoscel în care înălțimea este egală cu substratul deținut 8cm. Înălțimea prismei este egală cu 12 cm. Găsiți suprafața completă a prismei dacă partea laterală care conține baza triunghiului - pătrat.
Suprafața prismei va fi egală cu suma suprafețelor de baze și suma ariilor suprafețelor laterale, adică
- zona bazei prismei,
- suprafața laterală, cuprinzând o bază,
- suprafață laterală care cuprinde partea unui triunghi isoscel. (Ei sunt, ca o parte de bază sunt în consecință a triunghiului isoscel, iar cea de a doua parte sunt înălțimea prismei)
Deoarece fața laterală ce conține baza triunghiului, un pătrat, baza triunghiului este de asemenea egală cu 12 cm. (Baza triunghiului este fețele laterale simultan).
Astfel, cunoscând înălțimea și baza unui triunghi isoscel, puteți și alte aspecte ale spațiului găsi:
Picioarele, sunt, respectiv, (avem înălțimea, care este într-un triunghi echilateral, atât mediana
, cu fiecare dintre picioare forme un triunghi dreptunghic), prin teorema lui Pitagora:
,
3. În amprenta dreapta patrulateră prismă 144
, și o înălțime de 14 cm. gasi prisma diagonala.
Corect patrulater - un pătrat.
Prin urmare, partea de bază va fi egală cu
Acolo unde diagonal de bază prisme dreptunghiulare drept este egal cu
forme de prisme diagonale cu bază diagonală corectă și înălțimea triunghiului unghi-prisme. Prin urmare, teorema lui Pitagora diagonală predeterminată prisma patrulateră regulată va fi egală cu:
4. Luați în considerare o prismă dreptunghiulară regulată
, secțiunea diagonală din care - un pătrat. peste partea de sus
și coastele din mijloc AB si BC a avut loc avionul. Găsiți aria secțiunii transversale care rezultă, în cazul în care
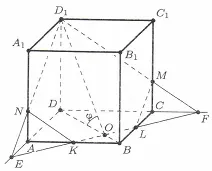
secțiune văzută în figură, Clădire unde K și L - ale punctelor mediane laturile AB și BC al prismei de bază, E și F - punctul de intersecție al liniei KL, respectiv, cu extensiile de părți DA și DC. Secțiunea este un pentagon
unde puteți găsi zona. Mozhnosnachala calcula zonele de triunghiuri
și apoi scăzând de două ori a doua zonă (triunghiuri ca și cea a primului triunghi
egal). Cu toate acestea, în acest caz, este mai ușor de utilizat formula:
la planul bazei prismei este un pentagon
, Am găsit-o zonă scăzând din aria pătratului
Zona VKL a triunghiului:
Lăsați BD bază diagonal traversează segmentul KL la punctul O. Deoarece
(Conform teoremei trei perpendicularele), atunci
- unghiul diedru liniar KL.
Unui triunghi dreptunghic
teorema lui Pitagora, avem:
5. Dana prismă dreapta:
,
. Găsiți înălțimea prismei.
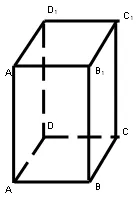
P = perimetrul bazei 8 cm.
6. Motivul pentru care cutia este pătrată. Unul dintre baza superioară vârfuri echidistant față de toate nodurile bazei inferioare și se află la o distanță b de la această bază. Partea de jos este. Găsiți suprafața completă a casetei.
- o cutie cu bazele
,
și marginile laterale
, Și ABCD - pătrat cu latura a. vârf
echidistant față de nodurile A, B, C și D, iar distanța de la vertexul
la planul de bază ABCD este egal cu b. deoarece punctul
echidistant față de vârfurile ABCD pătrat, acesta se așază pe perpendicular pe planul ABCD care trece prin centrul O al pătrat. Perpendicular a scăzut de la punctul O pe latura BC, trece prin M. sa mijlociul de teorema trei perpendicularele
. Unui triunghi dreptunghic
.
În cazul în care S - suprafața totală a casetei
.
7. Dovedește că în cazul în care planul de secțiune transversală a paralelipipedul este un poligon cu un număr de laturi mai mare de trei, atunci acest poligon este laturile paralele.
La aproximativ paralelipipedice trei perechi de fețe paralele. În cazul în care avionul se intersectează cu mai mult de trei fețe, apoi cel puțin două laturi ale secțiunii transversale poligonale sunt în părți opuse ale cutiei. Prin teorema la intersecția a două planuri paralele de a treia, cele două părți sunt paralele.
8. paralelipiped
linia ABCD - un pătrat cu laturile de 5, o nervură
5 precum și această nervură formează cu marginile AB și unghiurile AD
.
egale între ele, aceasta înseamnă că înălțimea
această piramidă trece prin centrul cercului circumscris despre baza ABD. precum și mijlocul de ipotenuză sale BD, adică - ABD dreptunghiular triunghi, punctul O centrul de ABCD pătrat. Unui triunghi dreptunghic
echidistant față de vârfurile C și D, deci este proiecția ortogonală K pe ABCD avionul la sol este, de asemenea, echidistant față de C și D, și, astfel, se află pe perpendiculara pe segmentul CD. ca
||
=
- un dreptunghi, deci OK =
= 5. KO va continua să taie până la intersecția cu segmentul AB de la punctul M. Apoi, M - punctul de mijloc al AB și MK = MO + OK =
. De la MKB și triunghiuri unghiulare
9. La marginea AD și diagonală
preluate punctele M și N, în plus, linia MN este paralelă
și AM: AD = 1: 5. găsi raportul
.
Fie P - centrul ABCD paralelogram. avion
- Prism cu baze
numita n - prismă de cărbune.
- Perpendicular trase din orice punct al unei baze într-un alt plan de bază, numit înălțimea prismei.
Dacă marginile laterale sunt perpendiculare bazele prismei, prisma este numită directă altfel - înclinată. Înălțimea prismei drepte este marginea sa laterală.
- Prism se numește regulat în cazul în care baza sa - poligoane regulate.
Dacă baza prismei este un paralelogram, este numit un paralelipiped. În toate aspectele cutiei - paralelogram.
- Face din cutie, fără noduri comune sunt numite opuse.
- Paralelipiped ale cărei margini laterale sunt perpendiculare pe planul de bază, numită paralelipipedului directă.
- În caseta toate fețele laterale ale bazei dreptunghiuri și paralelogram. Dacă toată fața caseta - dreptunghi, este numit un paralelipiped dreptunghic.
- Lungimile trei dintre margini, care se extind de la un nod, numit dimensiunile unui paralelipiped dreptunghiular.
- Paralelipiped toate cele trei dimensiuni sunt egale se numește un cub.