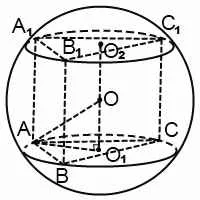
Prism se înscrie într-o sferă
Prism este înscris în minge, în cazul în care toate nodurile sale se află pe suprafața bilei (pe teren). În acest caz, se spune că mingea este descrisă despre o prismă (sau prisme in apropiere de sfera descrisă).
Prismă poate fi înscris într-o sferă dacă și numai dacă, atunci când
1) prisme drepte;
2) în apropierea bazei sale poate fi descrisă ca un cerc.

Rezultă că mingea poate fi înscris prisme triunghiulare drepte, prisme regulate.
Deoarece patrulaterul poate fi înscrisă într-un cerc, în cazul în care suma unghiurilor opuse egală cu 180º, prisma rectangulară drepte poate fi înscris într-o sferă numai sub această condiție.
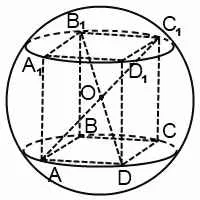
În special, paralelipipede descrise balon poate fi de aproximativ paralelipipedic numai. centrul bilei în acest caz - până la punctul de intersecție al diagonalelor cutiei.
În general, centrul sferei circumscris despre prisma se află pe un jumătatea înălțimii prismei care trece prin centrele cercurilor din jurul bazei sale. Centrul de minge poate fi descrisă în prisma, prisma și se află la fața sa laterală.
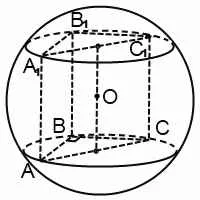
De exemplu, pentru o prismă triunghiulară, în care unghiul ABC - liniar descris centrul mingii se află la marginea laterală, la o înălțime care se conectează punctele de centru ipotenuzei prisma in motivele.
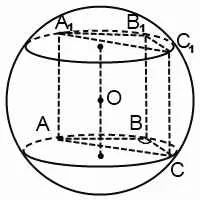
În cazul în care unghiul ABC - tocit, centrul sferei circumscris despre prisma triunghiulară a prismei este localizat.