Prezentarea pe conceptul de formă pătrată și dimensiunea sa

Prezentarea pe tema: „... Conceptul de formă pătrată și dimensiunea sa Care este zona din care figura Proprietăți pătrat este numit egal Ce cifra menționată de Ce egal cifra ...“ - Transcrierea:

1 Conceptul de formă pătrată și dimensiunea sa. Care este zona. Proprietati. Care figură se numește egal. Care sunt cifrele menționate de egal. Care sunt cifrele menționate equidecomposable. Unitatea de suprafață. Formula zona dreptunghiului, pătrat. Ce valoare se numește un scalar. Ce este reticulatia? Learn: Amintiți-vă:

2 Unități de măsură suprafață: 2 mm, 2 cm, dm 2, m 2 km2, m. 1 m = 2 m 1 m 2 = m 1 2 cm2 = 100 1 dm 2 km = m 2 2 dreptunghi pătrat este egală cu produsul dintre lungimile laturi adiacente ale acestora. 5. 3 = 15 (pătrate) S = a b Când a = 5, b = 3, obținem: S = 5. 3 = 15 (cm 2) Suprafața de pătrat este egală cu pătratul lungimii laturilor sale. S = o cm2 Feb. 15 și

3 Valoarea care este determinată de o valoare numerică numită o valoare scalară. (Lungime, arie, volum, masă, timp, prețul și cantitatea) și b instrument de 1cm, cu care își găsesc o valoare aproximativă a zonei este numit un mozaic. 15 cm S = ab 2 Când a = 5, b = 3, obținem: S = 5. 3 = 15 (cm 2)

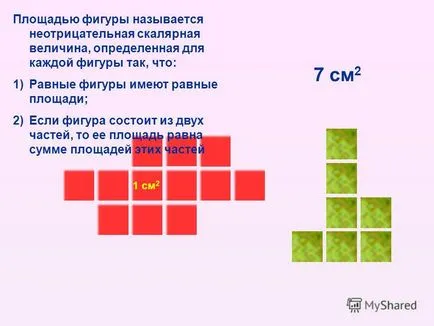
April 1 cm2 suprafață a figurii este numită o cantitate scalar nenegativ definită pentru fiecare formă, astfel încât: 1) forme Egale au zone egale; 2) Dacă cifra este format din două părți, suprafața sa este egală cu suma suprafețelor acestor porțiuni 7 cm2

5 Proprietățile zonelor de figuri plane. Figura 1. Dacă egal, apoi egală cu valoarea numerică a zonelor lor, adică. E. F 1 = F 2 S (F 1) = S (F 2) 2. Dacă cifra F este compusă din figuri din F 1 și F 2, valoarea numerică zona a figurii este suma valorilor numerice ale zonelor de cifre F 1 și F 2, respectiv. S (F 1, F 2) = S (F 1) + S (F 2) 3. Unitatea valoare numerică zonă pătrată luată egală cu 1, și anume S (E) = 1. 4. În zona unității înlocuind valoarea numerică a unei cifre crește aria F (scăderi) ori de câte ori noua unitate este mai mică (mai) vechi. 5. Dacă cifra 1 face parte din F F figura 2, valoarea numerică a ariei de figura F 1 nu este mai mare valoarea numerică a zonei F figura 2, și anume F 1 F 2 S (F 1) S (F 2)

6 Găsiți zona pe blatul a cărui lungime este egală cu 10DM și lățimea - 5cm. Având în vedere: a = 10DM, b = 5 cm. Găsiți S. Soluție. S = a b. 10DM = 100cm. S = 100 * 5 = 500 (cm2). SARCINĂ 1.

Lungimea coridorului 7 școală este 28m, iar latimea este de 4 ori mai puțin. Care este zona coridorului? Având în vedere: a = 28m, b - 4 ori mai Find S. Solution. S = a b, b -. b = 28. 4 = 7 (m). S = * 7 = 28 196 (m 2). Răspuns: 196m 2 SARCINĂ 2

Localizați aria figurii 8, prezentată mai jos: 5cm 3cm 4cm 4cm * 3 + 5 5 * 4 + 4 * 4 = = 51 (cm 2) Rezolvarea problemei (cu diverse metode):

9 4cm S = 4 * 4 = 16 (cm 2) S = a.aS a.a. = S = a 2 S n = 2 6a S = 6 * 4 2 = 96 (cm 2) SARCINA 4: găsi suprafața totală a cubului. A: 96 cm 2

10 Cele două figuri sunt numite egale, dacă una dintre ele vă poate pune pe un al doilea, că aceste cifre coincid.

11 A D C B K L M N poligoane equidecomposable sunt numite în cazul în care acestea pot fi împărțite în părți egale, respectiv. S = S 1 + S 2

12 OBIECTIVUL 5 6cm 12cm 3cm dacă zonele sunt egale? Două figuri cu suprafețe egale, numite de egale. Este adevărat că cifrele equidecomposable zonă întotdeauna egală? Este adevărat că cifrele sunt întotdeauna egale equidecomposable? Este adevărat că oricare două poligoane de suprafață egală sunt întotdeauna equi? (Casa. Sarcina. L.P.Stoylova, p)

13 Calculați formele de suprafață în cazul în care suprafața fiecărei celule este de 1 cm Algoritmul de calcul 2 suprafață folosind mozaic. paleți 1.Nalozhit la figură. Numărul 2.Soschitat și celule întregi din interiorul formei. Numărul 3.Soschitat în celulă aparținând figura în parte. 4.Soschitat valoarea aproximativă a zonei: S a + a 2 (atunci când un număr este impar, creșterea sau descrește prin 1). S 1 = S 2