plan direct și geometria euclidiană

Mai multe mii de matematică încearcă, pe de o parte, pentru a dovedi a cincea postulatul lui Euclid, dar pe de altă parte, mă întreb de ce a fost adăugat la primele patru Euclid.

postulat a cincea a fost întotdeauna considerată de prisos.

Una din modul său de redactare citește - „Pe plan prin punctul, care este o linie dreaptă, puteți desena doar o singură linie dreaptă paralelă cu acest lucru.“

Recall adoptat de definiții și proprietăți Euclid:

Definiția „punct este că nu are nici o parte“, rezultă că punctul este un segment de linie a cărei lungime este egală cu lățimea sa. În consecință, punctul face parte dintr-un drept sau un caz particular al liniei de afișare, și în același timp, lungimea și lățimea acesteia nu sunt egale cu zero, deoarece, în acest caz, punctul nu ar exista;

Definiția „Direct există o astfel de linie care este în mod egal tuturor punctelor“ ale definiției precedente că o linie dreaptă - un plan, a cărui lățime este egală cu lățimea punctului.

Prin urmare, o linie dreaptă - partea plană sau un caz particular, planul de afișare;

Definiția „un plan de suprafață, care este la fel pentru toate culcat direct pe ea“ implică faptul că planul poate consta din puncte, linii sau alte linii de planuri coincide cu acest lucru.

Rezultă că planul este conceptul de bază, și punctul și linia este un caz special al unui avion.

Continuând să argumenteze în aceeași ordine de idei, vom obține gândul răzvrătire, în cazul în care conceptul de bază este format din cazuri individuale, conceptul ar trebui să reprezinte un caz special.

În planimetrie Lobachevsky-Bolyai printr-un punct în afara liniei pe planul poate conține orice număr de diferite linii paralele la acest lucru. Aceasta este - o axiomă.

În planimetrie Riemann printr-un punct în afara liniei nu poate exercita nici o linie paralelă cu acest lucru. Această afirmație, de asemenea, axiomatizat. S-ar părea că poate fi subversiv în aceste axiome? În cazul în care pot fi inexacte, pe care atât de mulți ani șicane mulți oameni de știință? Inexactitate se află într-o singură definiție, iar această definiție - conceptul de „avion“.

Postularea această definiție, ca un plan absolut, ne aflăm într-o lume bidimensionala ireal baronului Munchausen.

În lumea reală tridimensională - Un avion este o suprafață cu o rază de curbură tinde la infinit.

Acest lucru implică faptul că există o linie directă, care este aceeași pentru toate punctele de suprafață cu o rază de curbură.

Raza de curbură a unui plan, și cu ea linia poate fi orice și definită de el specifică forțelor care acționează asupra avionului în zona curbei avute în vedere și nu dreptunghiulară.

Prin urmare, punctul reală, având o lungime, lățime și grosime este, de asemenea, o suprafață curbată. Pentru a respinge acest lucru, încercați să găsiți o secțiune dreaptă pe suprafața unui cerc sau sferă.

Poate că acest lucru este ceea ce este pusă la îndoială în geometria lui Euclid, introducerea geometriei a cincea postulat. postulat a cincea atașat euclidiene proprietăți plane suprafață complet plană. Introducerea conceptului de curbură afișează geometria euclidiană dintr-o lume plată bidimensionala a ireale lumea reală tridimensională a curbei.

Bidimensionala geometria euclidiană absolut plat devine un caz special, cu condiția ca raza de curbură a planului considerat sau curba tinde spre infinit.

In timpul lui Euclid, probabil, a avut nici o idee despre curbura spațiului, și chiar Pământul însuși este văzută ca o suprafață perfect plană.

Cu toate acestea, Euclid, probabil, nu au fost de acord cu această definiție.

Declarație în momentul în care Pământul este o suprafață curbată, sau mai mult mingea nu ar fi fost interpretate corect.

Probabil, al cincilea postulat lui Euclid a trimis un „mesaj criptic“ pentru viitorul omenirii, arătând că geometria sa cu un plan care nu totul este în regulă, că ea a inventat - ipotetic, al cincilea postulat lui.

Postularea un plan absolut, Euclid a dat omenirii capacitatea de a crea un convenabil și simplu de aplicat: geometrie, matematică, fizică, și astfel pune bazele pentru saltul în întinderea nesfârșită a spațiului curbat.

Recunoașterea faptului imposibilității existenței unui plan absolut, asta e, probabil, piatra de temelie a creării de noi geometrie, fizică, matematică, și calea de cunoaștere a universului.

triunghi Cu toate acestea, știința este încă înclinat Pitagora, construit pe un plan absolut euclidiană geometria, este baza teoriilor recunoscute la nivel internațional care descriu structura universului.

Ia Lorentz să le transforme în valoare √ 1 v 2 / c2 obținut din dreptunghiul pitagoreic.

Acest lucru este contrar literei și spiritul teoriei curbarea spatiului. în care nu există plat cameră triunghi unghi dreapta, perfect linii drepte și suprafață perfect plană.

Din nou, amintiți-vă Euclid și punctul său de definiție.

„Ideea este aceea care nu are părți.“ În lumea reală, punctul este un corp geometric.

Postulatele lui Euclid nu spune nimic despre grosimea punctului.

În lumea reală nu poate indica prezenta cel mai mic cerc cu o grosime lipsă.

Dacă adăugăm la definirea termenilor este, de asemenea, grosimea ei, atunci trebuie să fie cea mai mică minge.

În acest caz, nu putem profita de un triunghi plat al lui Pitagora nu au grosime.

La punctul de-castron, ca și cum nu am reduce dimensiunea sa, triunghi dreptunghic va avea trei unghiuri drepte, iar acest triunghi nu va fi în măsură să devină plat.

Neglijând a doua comandă de valoare mică, atunci când triunghiul este înlocuită cu o suprafață curbată a unui triunghi dreptunghiular, plat în microcosmos duce la erori enorme.

Efectuarea calculelor pentru suprafețe traiectorii a căror rază de curbură tinde spre zero, obținem care tinde spre triunghi zona zero euclidiană și valori de magnitudine Lobachevskian de ordinul al doilea, adică zonele de diferență sau lungimi în aceste geometrii, presupune o valoare ușor nu este egal cu triunghiuri pătrate sau distanțele dintre puncte.

Este ușor de imaginat această diferență este suficientă pentru a construi un model simplificat (Figura 1) bidimensional triunghiul euclidian în tridimensional triunghi Lobachevsky.

Aria triunghiului ABC Lobachevskian S = 4 πR 2/8 = 2/2 πR

Piața euclidiană triunghi, dreptunghi calculat pe baza Pythagoras S ABC = R2√3 / 2

Ca în cazul în care R nu tinde la zero, diferența este o zonă plană a unui triunghi și triunghiul de pe minge va fi despre diferite:

Ignorați această diferență și să presupunem că această magnitudine inexactitate de ordinul al doilea, care nu poate lua în considerare, nu este în mod clar corectă.

Același lucru se întâmplă și cu calea de mișcare a punctului A de la infinit la zero, - punctul B unde raza de curbură tinde spre zero (figura 2).

La porțiunea unde R → ∞ (Fig.2 stânga) picior AB, dacă aplicăm triunghiul drept pitagoreic ipotenuza substanțial egală și vom intra fizica newtoniană

In segmentul AB, unde R → 0 (Fig.2 dreapta) piciorul AB transformat într-o lungime de coardă L. care se calculează cu formula:

L 2 = a (2R - a).

Concluzia acestei formule arată încă vIIIveke în cartea chineză „Matematica în nouă cărți“ în problema indian matematikaVIIveka Bramagupty.

Descrierea traiectoriei electronului și spin pe baza curbelor tridimensionale reale și triunghiuri de volum. și nu pe baza a două-dimensionale dreptunghiuri drepte și plane poligonale permite matematicieni pentru a obține în interiorul atomului și pentru a descoperi secretele spațiului evaziv.

Recunoscând contribuția inestimabilă de fizicieni care au lucrat până de-al treilea mileniu, trebuie să admitem că ele nu sunt în măsură să descifreze mesajele secrete ale lui Euclid stabilite de acestea, în a cincea postulatul.

Model de materie și spațiu, creat pe baza unui dreptunghi dreptunghiular al lui Pitagora, ar trebui să recunoaștem bidimensional.

Al treilea mileniu trebuie să fie un mileniu al unui cadru care descrie reale modele tridimensionale ale spațiului curbat și a materiei.

postulăm Fifth Euclid 3 spațiul D.

Reprezentați a cincea postulăm Euclid, în general, în spațiul tridimensional.

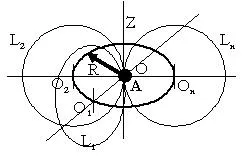
Prin A (Fig.3), având în vedere planul O1. având o rază de curbură care tinde la infinit, cu centrul O1. trage o linie L 1, cu o rază de curbură care tinde la infinit, și care coincide cu centrul de curbură O1 plane.

Mutăm centrul curburii punctului O2. și prin punctul A aparținând liniei L 2. planul O2. cu centrul de curbură O2 avionul.

După cum se poate vedea direct L 1. L 2. nu se intersectează într-un punct comun A.

Astfel, este posibil să dețină un număr infinit de linii paralele L 1. L 2. ..., L n → ∞ care nu aparțin unui anumit plan, dar având un punct A comun, cu condiția ca coordonatele centrului de curbură O1 a fiecărui plan. O2. ..., G n → ∞, descrie un cerc pe raza de curbură R → ∞ în jurul axei Z.

Axa Z este comune pentru toate planurile tangente luate în considerare.

În acest caz, vom obține o formă tridimensională a unui tor, cu egalitatea R. În general, R poate fi o valoare excelentă.

Într-un spațiu real fizic, raza de curbură nu este infinit, ci forță limitată, determinată de proprietățile fizice ale mediului de mediu și reacția zonei considerate în alte zone. Aceste proprietăți cauza deformarea planului de curbură ca raza oricare și toate axele de simetrie.

Din al cincilea postulat următoarele condiții:

1. Coordonatele Z plan, și, prin urmare, un punct de vedere directă și definite ca aparținând planului sunt egale.

2. Unul dintre X sau Y coordonate definit de puncte care nu aparțin liniei.

3. Direct are un singur grad de libertate.

4. Centrul de curbura a unei linii paralele cu un dat, o singură axă poate fi mutat pentru a se conforma paralelism.

Prin urmare, al cincilea postulat al lui Euclid, este un caz special, care descrie singura cale de ieșire din nenumărate.

Pe plan cu o rază predeterminată de curbură printr-un punct, care este o linie dreaptă. puteți desena doar o singură linie dreaptă paralelă cu aceasta, în care cel puțin una din coordonatele centrului de curbură nu coincide cu coordonatele centrului de curbura originale.

Această interpretare a cincea postulat descrie, în general conducta spațială (Figura 4), cu o rază de curbură R → ∞.

Introducerea noțiunii de curbură în descrierea avionului și drept, conduce la o concluzie paradoxală:

Orice linie cu continuarea ei fără sfârșit a unei curbe închise.

Într-adevăr, în cazul în care o linie dreaptă este raza de curbură, aceasta înseamnă că există un cerc la care aceasta face, indiferent de raza, până la infinit.

Prin urmare, curba dreaptă fără început și fără sfârșit.

Curve, originar de la infinit și a făcut drumul lor, krutanuvshis de spațiu infinit, din nou, se duce la infinit.

Ca o linie dreaptă poate fi distinse una de alta?

Dacă luăm coordonatele începutul și sfârșitul liniei, atunci ele sunt infinit incerte.

Iar dacă comparați razele de curbură a „direct“?

În acest caz, vom fi imediat capabil să distingă o linie de alta.

În lumea fizică reală, toate desigur. De aici razele de curbură ale „avioane“ „directe“ și sunt finite.

Asta înseamnă că despre finitudinea universul nostru?

La urma urmei, în conformitate cu geometria de construcție a modelului curbei se dovedește că, dacă depăși avionul cu o rază de curbură tinde la infinit este posibil pentru a ajunge la lumea interlopa. Cu toate acestea, de-a lungul modul în care ne vom întâlni MAJORA tangentă absolut direct la curba.

O linie perfect dreaptă în natura reală nu există (a se vedea. De mai jos).

În principiu, „trage“ o geometrie în care este posibil.
Este suficient pentru a profita de geometria Riemann.
Cu toate acestea, se pune întrebarea aici.
Este posibil să se deplaseze în această geometrie?
În acest caz, trebuie să recunoaștem că există o accelerație centrifugă, adică deplasarea accelerației cu raza negativă a vectorului curbură.
Mișcarea fizică reală are loc după aplicarea puterii pulsului (IS), în mărime ce depășește mărimea forței de reacție a acting câmpului undei pe corpul inerțial în stare de repaus.
Se pune întrebarea.
Pentru unii cale, există o mișcare sub influența IS
Prin centrifugă sau centripetă?
Această întrebare este relevant faptul că răspunsul la care determină geometria ar trebui să fie folosit pentru a descrie traiectoria.
Dacă această mișcare centripetă, traiectoria curbei trebuie descrisă de geometria reală a Lobachevsky. Aceasta este, centrul de curbură se află în interiorul cercului inscris.
Dacă această mișcare centrifugală, traiectoria mișcării trebuie descrisă curbe imaginare geometrie Riemann. Aceasta este, centrul de curbură se află în afara cercului înscris.

De exemplu, ia în considerare deplasarea rachetei în timpul accelerării.

În timpul lansării rampa de lansare a razei de curbură a traiectoriei rachetelor este egală cu raza Pământului R H (Fig.5).
După cum se știe, în timpul rachete de accelerație rămâne pe orbită în jurul Pământului, dacă nu este prima viteză cosmică este depășită.
Aceasta, la rândul său, înseamnă predominarea forțelor centripete ale intensității câmpului gravitațional generat Globe.
Traiectoria rachetei în timpul acestei mișcări, cu o rază de curbură R centripetă a lacului îndreptat spre Pământ. La atingerea vitezei de evacuare racheta trece dincolo de acțiunea câmpului gravitațional al Pământului.
Asta înseamnă că traiectoria rachetei a devenit centrifuge?
Răspunsul este evident - nr.
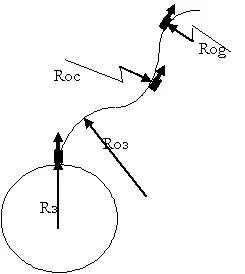
În acest caz, traiectoria rachetei determină câmpul gravitațional al soarelui. Traiectoria rachetei la acest stânga centripetă, dar cu o rază de curbură R oc îndreptate spre soare. Adică, se schimbă numai poziția centrului de curbură.
Același rezultat vom obține, având în vedere a treia viteza cosmica la care zboara rachete de-a lungul razei de curbură a Rog. Centrul de această locație a razei determină centrul galaxiei etc.
Astfel, în considerare orice mișcare, nu putem găsi natura și tipul forțelor centrifuge.
Recunoașterea existenței forței centrifuge conduce la recunoașterea existenței vieții de apoi și posibilitatea de mișcare pe o traiectorie imaginară care contrazice existența lumii reale.
Mai mult, pentru a trece de la geometria Euclid, cu raza reală geometria R. Riemann cu o rază imaginară - R. să fie depășită tangent complet drept la curbura care se străduiesc linie dreaptă cu o rază de curbură infinită R Fig.6.

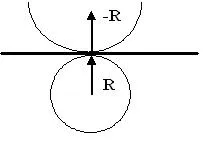
Pentru a depăși tangenta în mișcarea de tranziție de la real la geometria Lobachevskii mișcarea geometrie Riemann imaginară a centripet curbat trebuie să se întoarcă mai întâi într-o linie dreaptă absolut, și abia apoi ajunge într-o altă lume - o mișcare centrifugă curbată.
Dar este absolut mișcare liniară implică egalitatea absolută a puterii de acțiune a forțelor de opoziție, care neagă posibilitatea oricărei mișcări.
Acest lucru este probabil să aibă o dovadă geometrică a absenței mișcării centrifuge.
Dar, după cum sa menționat mai devreme, mișcarea perfect tangentă dreaptă nu există. Aceasta este, materie, spațiu, în acest caz să dispară, pentru că dispar orice forțe.

F = Puterea acțiunii - forță de reacție = 0

Cu toate acestea, preponderența de opinie în lumea științifică cu privire la existența unor forțe centrifuge a condus la faptul că toate axele din aparatul matematic aplicat au o direcție de la centrul din figura 7, care este o linie imaginară, și nu în centru, real - direcția reală din figura 8.

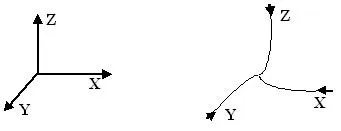
Figura 7 Figura 8
Imaginar, drepte, curbe, reale
axe axele de coordonate

Acest lucru conduce la erori semnificative în descrierea matematică a materiei, spațiu și fenomene naturale înregistrate.
Spațiul curbat, în timp ce conduceți pe un traseu curbat, axele ele însele trebuie să fie, de asemenea, curbilinie, Fig.8.
Definiția.
mișcarea de înaintare fizică este mișcarea valurilor, mediul, corpul, problema traiectoriei centripete cu o curbură îndreptată spre acțiunea forțelor de rezistență.
Centrul de curbură raza mișcare de translație fizică, în interiorul curburii, considerat traiectoria complot.
Pe baza celor de mai sus, se poate presupune că punerea în aplicare a vis prețuite omenirii - care zboară în spațiul nelimitat prevăzut, trebuie să mergeți la traiectoria de rachete cu o rază de curbură tinde la infinit, care este aproape de o linie dreaptă absolută care leagă două puncte în spațiu.