pendulă

Scopul acestei lucrări este: studiu de pendul matematic (în funcție de perioada de studiu oscilație a lungimii pendulului matematic și masa) și determinarea accelerației mediei sale cădere liberă prin pendul rotativ.

2. Introducere teoretică;

2.1. pendulului matematic pendul matematic este numit un sistem idealizată, format din fire imponderabilitate și inextensibil, care este suspendat concentrat în masă, la un singur punct. Destul de bună aproximare-zheniem pendulul matematic este un dispozitiv care reprezintă o minge mică-ing grele suspendat pe un fir lung și subțire (Fig. 1).

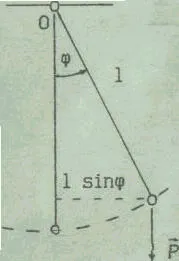
Deviația pendulului din poziția de echilibru va fi Funcțiilor, densitatea cu un unghi

, format fir cu verticala. Un pendul acționat de forțe externe: gravitațieși reacția suspensiei axei 0. în cazul unui pendul din poziția de echilibru, există un moment de forțăîn raport cu axa 0, care tinde să se întoarcă pendulul-a pus de echilibru. În cazul în care forța se află într-un plan perpendicular pe această axă, momentul său în jurul acestei axe este egală ca mărime cu produsul brațului forței (distanța de la axa la linia de-a lungul căreia acționează forța). Când pendulul este rotit cu un unghiîntr-o singură direcție forțatinde să se rotească în mod opus sistematic pui de somn. Prin urmare, semnul momentului forțeiîn ceea ce privește axa O este opusă unghiului de rotație al pendululuiISIN.

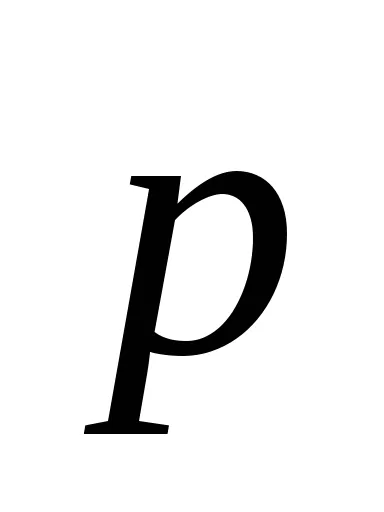
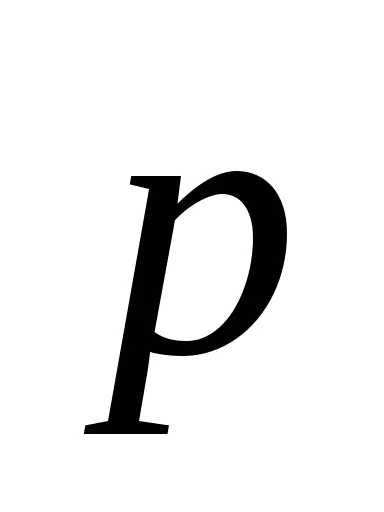
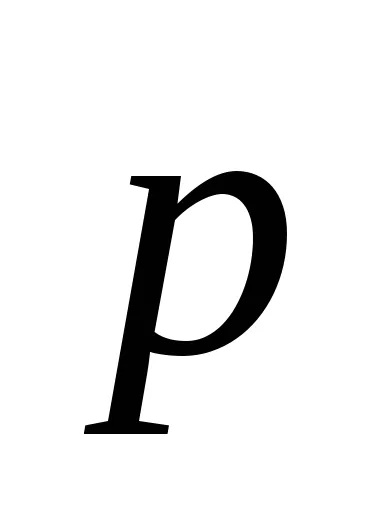
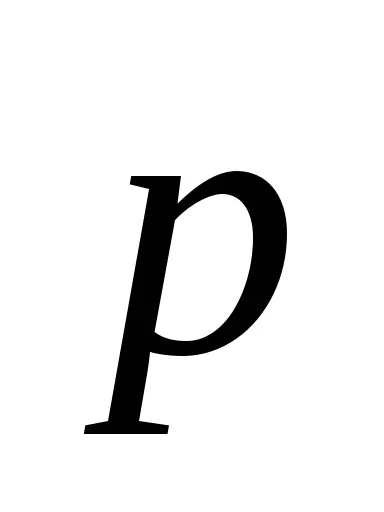
Expresia pentru M cuplul aplicat Mayat-nick este de forma

unde m - masa pendulului;

B - accelerația gravitațională;

mg - greutate (P = mg);

1 - lungimea pendulului.

Valoarea 1 sin

- braț al forței F în raport cu axa 0.

Pentru a studia oscilației pendulului trebuie să utilizeze legea fundamentală a dinamicii mișcării de rotație

unde J - momentul de inerție în jurul axei de rotație 0;

e - accelerația unghiulară a corpului (e = d 2

/ Dt 2. t - timp);

M - rezultând momentul (suma algebrică a tuturor momentelor care acționează asupra corpului forțelor externe în raport cu axa 0). Momentul de inerție J, care joacă același rol-kuyu în timpul mișcării de rotație a unui corp, care masa în translație, adică Este o măsură a corpului de inerție în timpul mișcării de rotație, și caracterizează rasele EFINIȚII-masa volumului corp.

Momentul de inerție în jurul axei masei punct material este produsul punctelor pe pătratul distanței r față de axa

Pentru corpurile extinse momentului de inerție este definită ca suma momentelor de inerție ale maselor elementare individuale Δmi, care pot fi împărțite corp, adică,

unde integrala se extinde pe întregul volum al corpului.

Momentul de inerție în raport cu axa suspensiei matematice balansoare 0. Conform formulei (3) este

Având în vedere valorile (1) și (5) legea de bază a dinamicii (2) ia forma unui pendul "

Impartind ambele părți ale ecuației (6) în 2 ml și introducerea desemnării

Noi obținem ecuația diferențială a oscilației matematice ma-yatnika

Ecuația (8) nu pot fi integrate în ceea ce privește timpul utilizând funcțiile elementare. Prin urmare, ne limităm la mici oscilații ale unui pendul, cu excepția păcatului

Apoi, în loc de 0 (8) vom avea următoarea ecuație diferențială aproximative pentru mici oscilații ale pendulului:

Soluția generală a acestei ecuații are forma

unde A și A - sunt constante arbitrare determinate de condițiile inițiale ale mișcării.

Amploarea A, adică cea mai mare valoare a unghiului de deviere de la verticală a pendulului, amplitudinea de oscilație se numește, - păcatul

a - frecvența ciclică (,v - frecvența de oscilație), argumentul () - F Zoe oscilație, iar cantitatea- fluctuații inițiale de fază (valori de fază stabilite la momentul inițial, adică la t = 0).

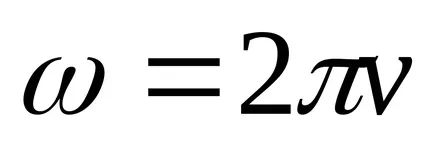
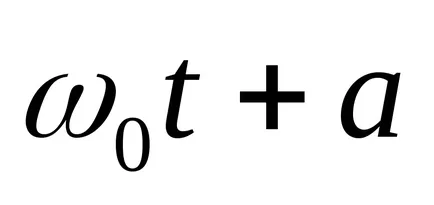
Astfel, pentru oscilații mici ale deviației unghiulare de pendul ma subiect variază în timp conform legii armonice. La unghiuri mari de deformare a pendulului va efectua mișcare complexă oscilatorie. După cum rezultă din ecuația (7), frecvența

pentru mici oscilații ale pendulului depinde de lungimea sa și pe accelerarea cădere liberă și nu depinde de masa pendulului. Perioada de mici oscilații ale unui pendul matematic, dacă înlocuiți are o valoare (7) va fi determinată prin formula

Perioada de oscilație a pendulului la amplitudini mici nu depind de amplitudinea. Această proprietate se numește oscilații izocrone ale unui pendul (descoperit de Galileo - în 1583).

pendul fizic numit corp solid, care se poate roti (swing) în jurul unei axe fixe sub acțiunea 0-prop Twain greutate (Fig. 2).

Luați în considerare oscilații în ceea ce privește forma și dispunerea elementelor de card-TION a masei pendulului. Pe pendulul deviat de la echilibrul de put TION, acționat de forțe externe: gravitatea

și reacția de suspensie axei 0. Friction în axa neglijare. Axa de suspensie de reacție nu are nici un moment despre axa de rotație. Momentul care tinde să se întoarcă pendulul în poziția sa de echilibru, este

,

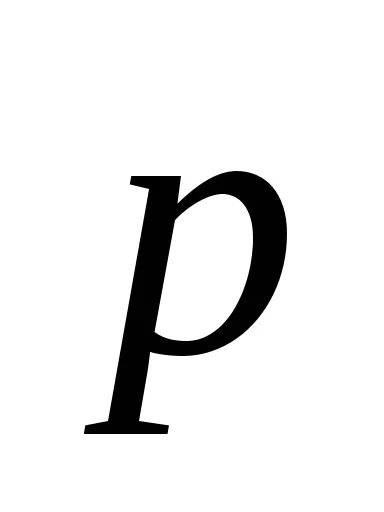
unde m - masa pendulului;

1 - distanța dintre punctul de suspensie 0 și centrul masei mayatni Single S.