oscilator armonic liniar în mecanica cuantică
Liniar armonic oscilator -
un sistem, care execută o mișcare de tensiune unidimensională sub quasielastic B-LY - (. a se vedea §142) un model folosit in multe probleme ale teoriei clasice și cuantice. Primăvară, INDIVIZI-cer și pendul matematic - cu-măsură clasice Osciloscoape armonice izolatori.
Energia potențială a oscilatorului armonic, al doilea (a se vedea. (141,5)) este
unde w0 - eigenfrequency oscilator, m - masa particulei. Osie-dependență (222.1) are forma unei parabole (ris.300), adică „Potential de bine“ în acest caz este parabolică. Mici oscilații de amplitudine clasă oscilator, determinată de energia totală E (vezi. Fig. 16). La punctul-tuple coordonatele ± xmax complet Ener-ogy E egal cu energia potențială. In aceasta, din punct de vedere clasic part-ca nu poate merge dincolo de câmp (-hmax. + Xmax). O astfel de retragere ar însemna că energia potențială este mai mare de jumătate de termen, ceea ce este absurd, din moment ce duce la tine, apa, energia cinetică a negativ-ing. Astfel, un tsillyator clasic este un „potențial
pit „cu coordonatele -xmax £ x £ xmax
„Fără dreptul de a ieși“ din ea.

Armonica oscilator în mecanica cuantică-urlet - un oscilator cuantic -
descrie ecuația Schrodinger (217,5), ținând cont de expresia (222,1) pentru energia potențială. Tor-stat și oscilator cuantic staționar sunt determinate prin ecuația Schrodinger a formei
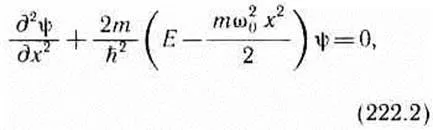
unde E - energia totală a oscilatorului. În teoria ecuațiilor diferențiale se dovedește că ecuația (222,2) re-cute numai cu propriile lor energii
Formula (222.3) arată că energia unui oscilator cuantic poate avea numai valori discrete, adică. E. cuantifică Xia. Energia este delimitată sub nenul, ca o „gaură“ dreptunghiulară cu „ziduri“ infinit de mare (a se vedea. §220), valoarea minimă a Ener-ologie E0 = 1/2 hw0. Existența unui termen minim de energie, - se numește energia punctului zero - este tipic sistemelor cuantice si este co-bout consecință directă neop-raport-determinare.
Prezența la zero oscilații înseamnă că particula nu poate fi pe partea de jos a „de potențial“, iar această concluzie este independentă de forma sa. De fapt, „picătură în partea de jos a sondei“ este asociat cu impulsul de zero-niem trase de particule și, în același timp, și incertitudinea acesteia. Apoi ne-determinarea coordonatelor devine arbitrar de mare, ceea ce contrazice, la rândul său, particulele rămân în „de potențial“.
Concluzionează că există putere la zero oscilații ale unui oscilator cuantice concluzii anti-rechit ale teoriei clasice, potrivit căreia co-cea mai mică energie, Koto-Rui poate avea un oscilator este egal cu zero (corespunzătoare repaus în poziția de echilibru a particulei). De exemplu, fizica clasica-LIC conduce la concluzia că
T = 0, energia mișcării de vibrație a atomilor într-un cristal trebuie să dispară. Prin urmare, ar trebui să dispară și împrăștierea luminii datorită atomilor vibrațional-niyami. Cu toate acestea, până când experimentul arată că intensitatea de împrăștiere a luminii este redusă atunci când temperatura nu este bine-lu, și tinde la o valoare limită, indicând faptul că T -> 0 vibrații atomice în cristal nu se rupe. Acesta este validat oscilatii-niem zero.
Formula (222,3), rezultă de asemenea că nivelele de energie ale oscilatorului armonic liniar sunt dispuse la distanțe egale între ele (ris.300), și anume distanța dintre nivelele de energie învecinate hw0 egal. în care valoarea minimă a energiei
O soluție riguroasă a problemei de oscilator cuantice duce la o altă ZNA, diferă considerabil de cursa-vizionarea clasic. Calculele Quantum-mecanice arată că particula poate fi detectăm să trăiască în afara zonei permise | x | £ XMAX (a se vedea figura 16 ..) întrucât punctul de vedere clasic, nu poate merge dincolo de câmp (-hmax, + x: max). Astfel, există o probabilitate nenulă de a găsi particula în regiune, care este clasic interzis. Acest rezultat (fără tine-apă) este prezentată în Fig. 301, unde este densitatea de probabilitate a cuantice unicitatii w oscilator pentru detectarea stării de n = 1. Figura arată că pentru oscilator cuantic Într-adevăr
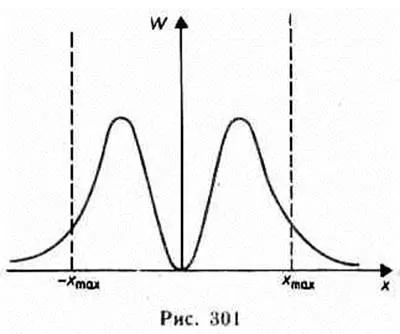
dar densitatea de probabilitate w are finite valori ale regiunii în afara clasic admisă | x | £ xmax. t. e. are Xia finit (dar mici) probabilitatea de a găsi o particulă în domeniul predela-
E „și potențial“. Existența unor valori non-zero mi limită w „potențial de bine“ este explicat microparticule coș-posibilitate care trec prin bariera de potențial (a se vedea. §221).
• Care sunt viteza de fază și de grup fotonului?
• În cazul în care, de ce și când condițiile DVX / vx <<1 и Dvx /vx »1 можно говорить о движении частицы
pe o anumită cale?
• Ca baza relației de incertitudine, explica prezența naturală a lățimii liniilor spectrale?
• Care este pătratul funcției de undă? De ce mecanica cuantică este o teorie statistică? Care este diferența dintre înțelegerea de cauzalitate în mecanica clasică și cuantică?
• Cum va potențial factor de transparență barieră cu creșterea lățimii sale în jumătate?
• Poate particula este în partea de jos a „de potențial“? Este determinată de forma „bine“?
• Care este diferența dintre descrieri mecanice clasice și cuantice de armonice oscilatoare-ra? Concluziile acestor descrieri?
28.1. fără particule se deplasează cu viteza. Demonstrați că relația
28.2. Electronul se mută la atomul de hidrogen al primei orbita Bohr. Presupunând că incertitudinea rată permisă este May 1% din valoarea sa numerică, pentru a determina coordonatele incertitudinii de electroni. Fie aplicat în acest caz, pentru conceptul de traiectoria de electroni? [Dx = 33 nm; nu]
28.3. y-function a unei particule este dată de y = (A / r) e -r / a, unde r - distanța particulei de
Power Center, o - constanta. Se determină distanța medie
28.4. Se înregistrează ecuația Schrödinger pentru un electron stările staționare situate în atom de hidrogen.
28.5. Electron este într-o formă dreptunghiulară „potențial de bine“ one-dimensional cu lățime infinit-l Sure „ziduri“ înalte. Determina treimea mijlocie a „gropi“, în cazul în care electronul este în stare probabilitatea de detectare a electronilor excitat de W (n = 2). INDIVIZI explica-ing sensul rezultatului, grafic detectare a densității de probabilitate a unui electron într-un anumit stat. [W = 0195]
28,6. Bariera potențial dreptunghiulară are o lățime de 0,1 nm. Se determină în electroni testamente minute diferență în energiile U-E, în care probabilitatea electronului care trece prin bariera va fi 0.99. [0,1 meV]