Optimizarea funcțiilor de una și mai multe variabile în Mathcad ptc

1. Funcție de căutare extremelor

Sarcini de căutare funcționează constatare extremelor înseamnă valoarea sa maximă (valoarea maximă) sau minimă (cea mai mică valoare) la un anumit domeniu de argumentele sale. Limitări ale valorilor argument care definesc acest domeniu, precum și alte condiții suplimentare ar trebui definită ca un sistem de ecuații și inegalități (sau). În acest caz, vorbim despre problema unei extremum condiționate.

Pentru a rezolva problemele de căutare de vârf și minim în Mathcad a construit funcția Minerr, Minimizarea si pentru a maximiza. Toate acestea folosesc aceleași metode numerice ca gradient funcția Find pentru a rezolva ecuații.

2. Funcțiile extremum ale unei variabile

Cautare extreme ale unei funcții include sarcina de a găsi o extremelor locale și globale. Ultimul este numit, de asemenea, probleme de optimizare. Să considerăm un exemplu specific al funcției f (x), prezentată în graficul din figura 2, în intervalul (-2,5). Acesta are un maxim la nivel mondial la granița din stânga a intervalului, minimul la nivel mondial, maxim local, minimul local și un maxim local, la intervalul de delimitare din dreapta (de la stânga la dreapta).

În Mathcad cu ajutorul funcțiilor încorporate rezolvă problema de căutare extremelor locale. Pentru a găsi maximul la nivel mondial (sau minim) este necesar, fie să calculeze mai întâi toate valorile lor locale, și apoi alegeți cea mai mare (cel mai mic) sau pre-scanarea cu o anumită etapă zona tratată pentru a alege un subdomeniu al celor mai mari (mai mici), valorile funcției și pentru a căuta extremelor la nivel mondial este deja în împrejurimile sale. Cea din urmă cale este plină de un anumit risc de a părăsi zona de alt extremelor locale, dar poate fi de multe ori de preferat din motive de economie de timp.

Fig. 1. Graficul de f (x) = x 4 + 5x 3 -10H

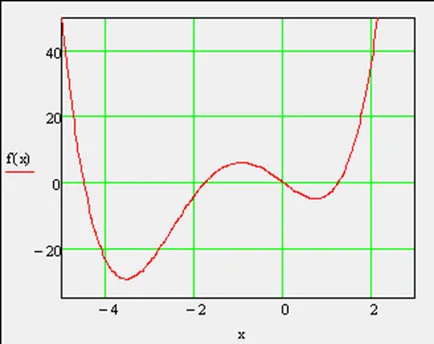
Se trasează funcția predeterminată (Fig.1). Prin grafica porțiuni vizibile ale extremelor locale ale funcției.

Există două funcții predefinite pentru a găsi locale Extrema, care poate fi utilizat atât în ​​cadrul unității de calcul, și în mod independent.

· Minimizarea (f, x1, ..., hm) - valori argument vector pentru care funcția f devine minimă;

· Maximize (f, x1, ..., hm) - valori argument vector pentru care funcția f atinge un maxim;

(. X1, ... hmm ...) f - funcția;

x1, .... XM - argumente asupra cărora minimizarea (maximizare).

Toate argumentele funcției f anterior pentru a atribui anumite valori, precum și pentru acele variabile care minimizarea, acestea vor fi percepute ca aproximarea inițială. Exemple de calcul o funcție extremum a unei variabile (figura 1), fără condiții suplimentare sunt prezentate în Listarea în Fig.2. Deoarece nu condiții suplimentare nu sunt introduse, căutarea se efectuează pentru toate valorile Extrema.

Fig.2. Căutare locală Extrema funcțiilor de o variabilă

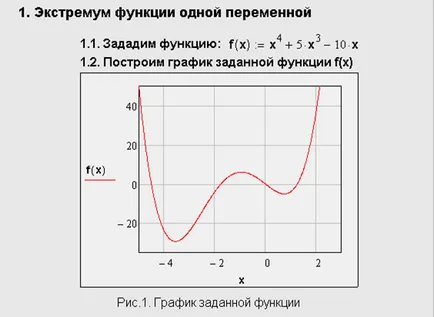
După cum se vede din lista, un impact semnificativ asupra rezultatului de selecție are o aproximare inițială, în funcție de care, ca răspuns emis diverse extremelor locale. În acest ultim caz, o metodă numerică nu face cu problema, ca o aproximare inițială x = -10 este selectat departe de zona de maxime locale, soluții de căutare și merge în sus f (x).

3. Optimizarea Constrâns

Problemele cu privire la o minimizare condiționată și maximizarea funcției extremelor ar trebui să fie incluse în unitatea de calcul, de ex., E. Acestea ar trebui să fie precedate de un anumit cuvânt cheie. Între Având în vedere și funcția de căutare extremum cu operatori booleeni înregistrate expresie logică (inegalitatea ecuației), să stabilească limite privind valoarea funcției argument să fie minimizate. Figura 3 prezintă exemple de căutare extremum condițional la diferite intervale definite de inegalitățile. Comparați rezultatele acestei liste cu cele două precedente.

Fig. 3. Trei exemple de funcția de căutare de optimizare constrânsă

Nu uita despre importanța alegerii abordării inițiale chiar în cazul extremelor condiționate. De exemplu, dacă în loc de condiție - 3<х<0 в последнем примере листинга задать -5<х<0. то при том же самом начальном х=-10 будет найден максимум Maximize(f,x) =-0.944. что неверно, поскольку максимальное значение достигается функцией f (х) на левой границе интервала при х=-5. Выбор начального приближения х=-4 решает задачу правильно, выдавая в качестве результата Maximize (f ,x) =-5 .

4. extremum funcției de mai multe variabile

Calcularea extremele unei funcții de mai multe variabile nu suportă principalele caracteristici, în comparație cu funcții de o variabilă. De aceea, ne limităm exemplul (Fig.4) găsirea minimul funcției afișate într-un grafic de suprafață tridimensională (fig. 4).

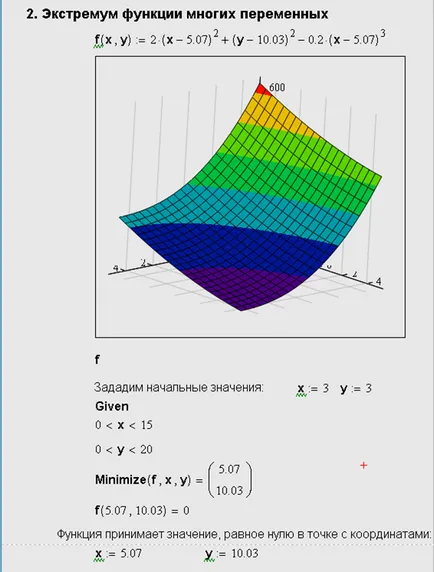
Fig. 4. Un minim de o funcție de două variabile

minim de căutare pot fi organizate cu ajutorul funcției Minerr. Pentru a face acest lucru în listă (Figura 4), este necesar să se schimbe numele funcției, pentru a minimiza Minerr. și după cuvântul cheie Dată fiind adăugați expresie egalează funcția f (x, y), valoarea în mod clar mai mică decât valoarea minimă, de exemplu f (x, y) = 0.