Metodele hook-Jeeves

3. Metoda modificată de Hooke-Jeeves

4. Schema bloc a metodei

5. O schemă bloc a unui singur studiu

6. Textul programului

7. Imprimarea rezultatelor programului de lucru

Pentru dezvoltarea de metode de căutare directă pentru determinarea funcțiilor minime și variabilele au fost cheltuite o mulțime de efort. Metodele de căutare directe sunt metode care sunt utilizate numai valori ale funcției. Considerăm că doar unul dintre ei în detaliu. Practica a arătat că această metodă este eficientă și aplicabilă unui număr mare de aplicații.

Luați în considerare funcția de două variabile. Linia ei de nivel constant 1 din Fig. 1

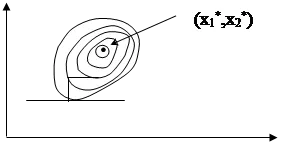
iar valoarea minimă este de la (x1 *, x2 *). Cea mai simplă metodă este de a găsi o metodă de coborâre. Din punctul A producem căutare minimă de-a lungul axei. în acest fel, vom găsi punctul B, la care tangenta la o linie paralelă cu un nivel constant axa. Apoi, prin căutarea din punctul B în direcția axei. Obținem punctul C, căutând paralel cu axa. obține punctul D, t. e. Astfel, am ajuns la punctul optim. Modul în care acest lucru evident iduyu poate fi folosit pentru funcții n-variabile.

În teorie, această metodă este eficientă în cazul unei singure minime a funcției. Dar, în practică, se dovedește a fi prea lent. Prin urmare, a fost dezvoltat mai multe metode complexe, care folosesc mai multe informații pe baza valorilor deja primite ale funcției.

Metoda Hooke-Jeeves a fost dezvoltat în 1961, dar este încă un foarte eficient și original. Căutarea constă într-o serie de explorare pașii care caută în jurul punctului de bază. pentru care, în caz de succes, ar trebui să căutare model. Acesta este utilizat pentru rezolvarea problemei de minimizare a funcției, fără a lua în considerare restricții.

Această procedură este prezentată mai jos:

A. Selectați inițial punctul de bază b1 și lungimea treptei H1 pentru fiecare variabila xj. j = 1, 2, ..., n. Următorul program pentru fiecare pas variabil utilizat h. dar modificarea poate fi de asemenea utile menționate mai sus.

B. Se calculează f (x), la punctul de bază b1 pentru a obține informații despre comportamentul local al unei funcții f (x). Aceste informații vor fi utilizate pentru a găsi o direcție potrivită de căutare pentru modelul prin care putem spera să se realizeze o reducere mai mare a valorii funcției. Funcția f (x) la punctul de bază b1. Acesta este după cum urmează:

1. Se calculează valoarea funcției f (b1), la punctul de bază b1.

2. Fiecare variabilă la un moment dat este modificată prin adăugarea lungimea pasului. Astfel, vom calcula valoarea funcției f (b1 + h1 e1), unde e1 - un vector unitate în direcția axei x1. În cazul în care acest lucru duce la o scădere a valorii funcției, aceasta se înlocuiește cu b1 b1 + H1 e1. In caz contrar, valoarea calculată a funcției f (b1 -h-1 e1), iar dacă este mai mic, atunci b1 se înlocuiește cu e1 -h1 b1. În cazul în care nici unul dintre pași făcuți nu reduce valoarea funcției, punctul b-1 rămâne neschimbat și analizează schimbările în direcția axei X2. t. e. este valoarea funcției f (b1 + e2 h2), și așa mai departe. d. Atunci când se va adresa toate variabilele n, vom avea un nou punct de bază b2.

3. Dacă = b2 b1. t. e. o descreștere a funcției nu a fost realizat, studiul se repetă în jurul aceluiași punct de bază b1. dar cu o lungime de pas redus. În practică, o etapă de reducere satisfăcătoare (etape) în zece ori lungimea inițială.

b1. o căutare este efectuată pe eșantion.

Q. Când căutați modelul utilizează informațiile obținute în cursul studiului, și pentru a minimiza funcția de căutare se termină în direcția unei probe date. Această procedură este după cum urmează:

3. Este rezonabil să se deplaseze din punctul de referință în direcția b2 b2 -b-1. deoarece căutarea în această direcție a condus deja la o scădere a valorii funcției. Prin urmare, vom calcula punctul caracteristică din eșantion

2. Apoi, studiul ar trebui să continue în jurul P1 (P i) litera.

3. În cazul în care cea mai mică valoare în etapa B, 2 mai mică decât punctul de bază b2 (în general, bi + 1), apoi a obține un punct de b3 bază nouă (bi + 2), apoi repetați pasul B 1. În cazul opus căutarea pentru modelul punctului b2 (bi + 1), și cercetări suplimentare în punctul b2 (bi + 1).

G. Terminarea acestui proces atunci când lungimea pas (pas lungime) va fi redus la o mică valoare predeterminată.

Metoda modificată de Hooke-Jeeves

Această metodă este ușor de modificat și pentru a ține seama de restricțiile .Bylo o propunere. că acest lucru va fi suficient pentru a rezolva problema de minimizarea funcției obiectiv pentru a atribui o mare importanță în cazul în care restricțiile sunt încălcate .K În plus, o astfel de idee pur și simplu, realizat de programare.

Trebuie să verifice dacă fiecare punct obținut în procesul de căutare. Ea face parte din constrângerile de câmp .Dacă fiecare. funcția obiectiv este calculată în mod obișnuit. În cazul în care nu. funcția obiectiv este atribuită o mare importanță. Astfel. căutarea va fi efectuată din nou în regiune admisă în direcția punctului minim în acest domeniu.

Metoda de text proscale modificat de căutare directă Hooke-Jeeves încercarea de a pune în aplicare o astfel de procedură. Problema în cauză are următorul cuprins:

pentru restricții x1

writeln ( 'funcție minimă egală', '', fb: 2: 3);

writeln ( 'număr egal de funcții de calcul', '', fe);

se repetă până la keypressed;

Programul de mai sus pune în aplicare această procedură. Unul sau două puncte sunt insuficiente pentru a determina punctul de plecare. Primul punct trebuie să fie întotdeauna selectate cu atenție. Calculator funcționează numai cu o precizie limitată și greșelile pot fi acumulate în procesul de calcule complexe, mai ales dacă pasul este lungimea „inconfortabil“. (În mod normal, vom evita „incomod“, în lungime, dar programul trebuie să fie puse în funcțiune și în astfel de situații.) Prin urmare, în linie. în cazul în care apare problema schimbării punctului de referință, vom evita reducerea lungimii pasului din cauza acumulării de erori prin introducerea de lungime pas egal

. Ne ține evidența în cazul în care se realizează cercetarea - în punctul de bază (H5 = 1, R5 = 0) sau punctul de probă (B5 = 0, P5 = 1). După cum se poate observa în practică, în cazul în care nu sunt luate măsuri de precauție cu astfel de program satisfăcător chiar și logica va fi inutilizabil.

În programul de mai sus, lungimea minimă a unui pas este

, dar poate fi schimbat. Pentru a monitoriza punerea în aplicare a procedurilor de programe implementate de imprimare a rezultatelor intermediare. sfaturi linie de ieșire și explicații pot fi eliminate pentru a crește rata de numărare.

Procedura de calculare calculează valoarea funcției obiectiv în acest caz. f (x1, x2) = 3x1 +-4x 2 1 x2 + 5x2 2

pentru restricții x1

Cel puțin egală cu 44, se ajunge la punctul (3, 1), sub x1 + x2 constrîngere = 4.

Pentru punctul inițial (4, 3) și lungimea pas. unitate. Programul a rezolvat cu succes problema de minimizare.

Mai jos este o listă a rezultatului programului de lucru:

Metoda modificată de Hooke-Jeeves

Introduceți numărul de variabile

Introduceți punctul de pornire x1, x2, ..., xn

Introduceți lungimea pasului dvs.

Funcția minimă este egală cu 44.000

Numărul de calcule este egal cu 74

Pentru punctul inițial (3, 4) și lungimea treptei. unitate. De asemenea, programul a rezolvat cu succes problema de minimizare.

Pentru punctul inițial (5, 6) și lungimea pas. unitate. problema nu este rezolvată. deoarece Programul sa oprit la punctul (1, 3). și anume constrângeri active. și a dat un rezultat incorect.

Rezultatele de imprimare ale programului de lucru prezentate mai jos:

Metoda modificată de Hooke-Jeeves

Introduceți numărul de variabile

Introduceți punctul de pornire x1, x2, ..., xn

Introduceți lungimea pasului dvs.

Valoarea inițială a funcției 375.000

Test de etapa 324.000

Test de etapa 253.000

Căutare model 155.000

Test de etapa 124.000

Test de etapa 81.000

modelat de căutare 1.70000000000001566E + 0,038

Test step 1.70000000000001566E + 0,038

Înlocuirea punctului de referință 81.000

Testul pas 60,000

modelat de căutare 1.70000000000001566E + 0,038

Testul pas 60,000

Înlocuirea punctului de referință 60,000

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Testul pas 60,000

Scade lungimea pasului

Funcția minimă este egală cu 60,000

Numărul de calcule este egal cu 89

rezultate dezamăgitoare similare au fost obținute pentru un punct inițial (5, 6) și lungimea pas. egală cu 0,5 soluție .Nevernoe a fost găsită la punctul (1.5; 2.5). Pentru punctul inițial (4, 3) și lungimea pas. egală cu 0,5, programul va funcționa corect. dar decizia greșită a fost primit la punctul (2.5; 1.5).

Problema este clară. Cu această metodă este imposibil să se deplaseze de-a lungul frontierei dintre limitările și convergența se realizează în primul punct de delimitare. în cazul în care există o decizie. problema totala de optimizare cu constrângeri este foarte dificil și de a oferi o metodă practică pentru rezolvarea nevoii de tratamente mai sofisticate. decât cele de mai sus.

1. B.Bandi „Metode de optimizare“

2. R.Huk. T.A.Dzhivs „Soluții de căutare directă pentru probleme numerice și statice,“ 212-219 secunde. 1961.