Metode de rezolvare a ecuatiilor neliniare
Cuvinte cheie: ecuatii neliniare, matematică aplicată, CAD de MathCAD, metoda lui Newton, metoda pas, metoda dihotomie.
Obiectiv: Pentru a studia metodele de rezolvare a ecuațiilor neliniare cu o singură necunoscută și le vor testa în lucrările experimentale.
- Analizeaza literatura de specialitate și de a alege căile cele mai raționale de rezolvare a ecuațiilor neliniare, care permite un studiu profund și asimila subiectul tuturor absolvenților de liceu.
- Pentru a dezvolta anumite aspecte ale metodelor de rezolvare a ecuațiilor neliniare cu utilizarea TIC.
- Exploreaza metode de rezolvare a ecuațiilor neliniare:
- Metoda de împărțire în două
Să presupunem că doriți să rezolve o ecuație neliniară a formei ecuației F (x) = 0. De asemenea, presupunem că suntem dat un interval de căutare [x0, x1]. Necesită intervalul de căutare [a, b] de lungime h, care cuprinde o primă rădăcină a ecuației, deoarece limita din stânga a intervalului de căutare.
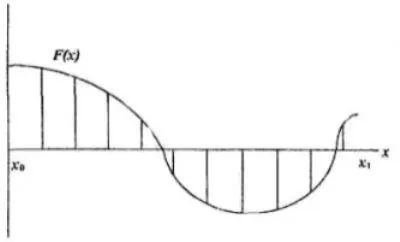
Fig. 1. Metoda pas
Pentru a rezolva o astfel de problemă în mai multe moduri. Metoda pas este cea mai simplă de metode numerice pentru rezolvarea inegalităților, dar pentru a obține o mai mare precizie necesară pentru a reduce în mod semnificativ pasul, și crește foarte mult calculele de timp. Algoritmul pentru rezolvarea ecuațiilor folosind această metodă constă din două etape.
În această etapă, porțiunile, fiecare dintre ele conținând numai o rădăcină a ecuației. Există mai multe opțiuni pentru punerea în aplicare a acestei etape:
- Setare substitut X (de preferință, cu unele pas destul de bine) și a vedea în cazul în care funcția își schimbă semnul. Dacă funcția este schimbat semnul, ceea ce înseamnă că zona dintre precedent și valoarea curentă a X este rădăcină (în cazul în care funcția nu modifică natura creștere / scădere, se poate argumenta că rădăcina acestui interval de unul).
- Metoda grafică. Programul de construcție și de a evalua la ce intervale este o rădăcină.
- Noi investigăm proprietățile unei anumite funcții.
În această etapă, valoarea rădăcina ecuației definită specificată anterior. De obicei, în acest stadiu, folosind metode iterative. De exemplu, metoda de împărțire în două (dihotomie) sau metoda lui Newton.
Metoda de împărțire în două
destul de simplă și rapidă metodă numerică pentru rezolvarea ecuațiilor bazate pe intervalul de contracție secvențială care conține o rădăcină unică de F (x) = 0 până la intervalul de timp până o precizie predeterminată E. Această metodă este folosită în soluția de ecuații pătratice și ecuațiile de grad mai mare. Totuși, această metodă are un dezavantaj semnificativ - în cazul în care intervalul [a, b] conține mai mult de o rădăcină, apoi utilizați-l să nu fie în măsură să obțină rezultate bune.
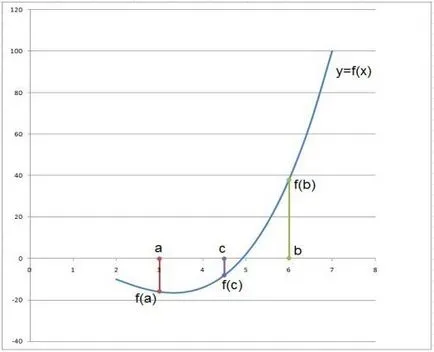
Fig. 2. Metoda de dichotomy
Algoritmul acestei metode este următoarea:
- să identifice o nouă aproximare a rădăcinii lui x în mijlocul intervalului [a, b]: x = (a + b) / 2.
- Găsiți valorile funcției în punctele a și x: F (a) și F (x).
- Verificarea stării F (a) * F (x) 0. Astfel, punctul cu x0 abscisă este ales. la care tangenta la curba y = f (x) în intervalul [a, b] intersectează axa Ox. Pentru primul punct x0 este convenabil de a alege unul dintre capetele segmentului.
Să considerăm algoritmul pe un exemplu specific.
Să presupunem că avem o crestere functiei y = f (x) = x 2 2 este continuu în intervalul (0, 2), și având f '(x) = 2x> 0 și f' „(x) = 2> 0.
În acest caz, ecuația tangentei are forma: y-y0 = 2x0 · (x-x0). Ca punct x0 alege un punct B1 (b; f (b)) = (2,2). Atragem tangenta funcției y = f (x) la punctul B1. și reprezintă punctul de intersecție al tangentei și punctul x1 axa Ox. Obținem ecuație tangent: y-2 = 2 · 2 (x-2), y =-4x 6. Punctul de intersecție al tangentei și Bivolul axa: x1 =
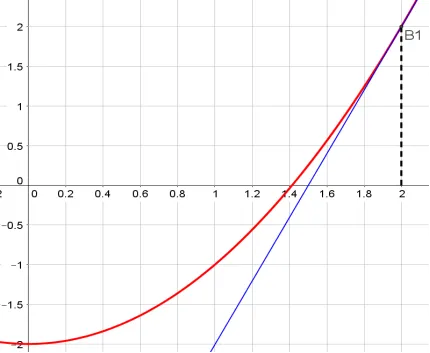
Fig. 3. Construirea unei prime tangentă la graficul funcției f (x)
Apoi vom găsi punctul de intersecție a unei y funcției = f (x) și perpendicular atras pe axa Ox prin punctul x1. Obținem punctul B2 = (1,5; 0,25). Din nou, tangent la funcția y = f (x) la punctul B2. și reprezintă punctul de intersecție al tangentă și Ox punctul x2.
Ecuația a doua tangentă: y = 2-2.25 * 1.5 (x-1.5), y = 3x - 4,25. Punctul de intersecție al tangentei și axa Ox: x2 =.
Apoi vom găsi punctul de intersecție a unei y funcției = f (x) și perpendicular atras pe axa Ox prin punctul x2. Obținem punctul B3, și așa mai departe.
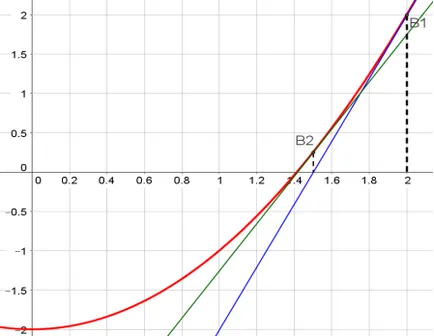
Fig. 4. Construcția unui al doilea tangentă la graficul funcției f (x)
Prima apropiere a rădăcinii este dată de:
Cea de a doua apropiere a rădăcinii este dată de:
=
A treia apropiere a rădăcinii este dată de:
Astfel, i -lea aproximare rădăcină este dată de:
Calculele sunt efectuate până la până la un meci de zecimale care sunt necesare în răspunsul, sau specificat de precizie e - la inegalitatea | xi-xi-1 |