Metoda de loci în soluționarea problemelor de construcție

Rezolvarea problemelor de HMT este după cum urmează:

A) problema este formulată astfel încât decizia sa vine în jos pentru a găsi piese care îndeplinește una sau mai multe condiții.

B) În cazul în care condiția este una, soluția problemei va fi un locus corespunzător. În cazul în care în cazul în care mai multe condiții, apoi, a aruncat unul dintre ele, vom obține o nouă problemă, a cărei soluție va fi una sau mai multe dintre HMT. Acest locus este cunoscut în mod obișnuit și ușor de construit.

B) Apoi, luând în considerare starea de aruncat și aruncarea înapoi în mare orice altă condiție, pentru a primi un nou locus.

D) Punctele sunt soluții de probleme (ᴛ.ᴇ. satisface în întregime condiționează sale ??) trebuie să aparțină atât primul și al doilea locus. Deci, ei trebuie să aparțină intersecția lor.

Sarcina are o soluție sau care nu se bazează pe faptul dacă sunt sau nu locusul au puncte comune. Acesta va avea cât mai multe soluții, există puncte de intersecție.

EXEMPLU 4.Postroit cercul tangent cercului de la punctul B, iar această linie MN. (Fig. 5).

Analiză. Să presupunem că problema este rezolvată, ᴛ.ᴇ. cercul cu centrul de satisface condițiile O1 ale problemei, ᴛ.ᴇ. tangent la cercul cu centrul în punctul O și în ceea ce privește linia dreaptă MN. Apoi, centrele cercurilor dorite se află pe OB linia (HMT numărul 6). Având de B tangent la cele două cercuri la intersecția cu MN în punctul R, obținem că unghiul dorit al cercului înscris în NKV. Prin urmare,

centru se află pe bisectoarea unghiului (HMT № 11); Bisectors unghiulare adiacente, obținem a doua soluție.

Clădire. Prin punctele B și D dețin o linie dreaptă. In continuare prin tangent la circumferința predeterminată. Obținem unghiurile și MACs BKN. Construirea unei bisectoare a unghiului. intersecția lor cu linia OB da centrele dorite ale cercurilor - O1 și O2. Construirea unui cerc cu centrul la O1 O1 în raza și un cerc centrat pe O2 O2 raza B.

Acest lucru rezultă din construcție.

Studiu. Numărul de soluții depinde de poziția relativă a cercului O și linia MN. Există trei cazuri.

1) Direct MN nu are puncte comune cu cercul. În acest caz, problema este, așa cum am discutat deja, cele două soluții. (Dezasamblați caz propriu, atunci când MN # 9553; IN).

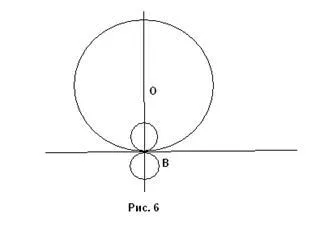
2) Direct MN tangente la cercul. În cazul în care contactul are loc la punctul B, atunci problema are infinit mai multe soluții (Fig. 6). Toate centrele cercurilor sunt căutate pe linia OB.

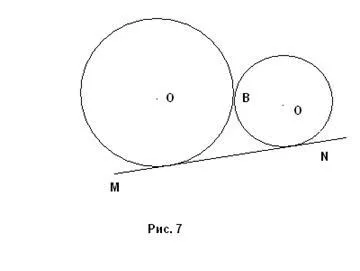
În cazul în care punctul B nu este același punct de tangență. Apoi, problema are o singură soluție (Fig. 7).

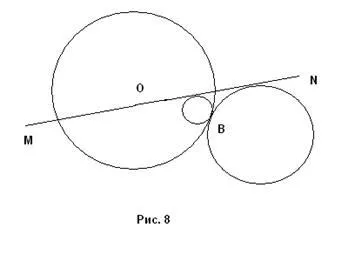
3) Direct MN traversează acest cerc. Dacă unul dintre punctele de intersecție coincide cu punctul B, atunci nu există soluții. În cazul în care MN nu trece prin punctul B, cele două soluții (Fig. 8).

EXEMPLU 5.Postroit triunghi și baza, o ha înălțime și lateral b.

Analiză. Să presupunem că triunghiul ABC este construit și are Soare = a, CA = b și vysota͵ coborât din vârful A, este ha. Atunci setul de soare ?? vârfuri de ex triunghiuri cu

o o ha înălțime de bază și va sta pe două linii paralele la soare și distanțate de acesta printr-o ha distanță (HMT № 10).

Mai mult, din moment ce CA = b, atunci punctul A este situat la o anumită distanță de punctul C, ceea ce înseamnă că se află pe un cerc de rază b centrat în punctul C (HMT № 1). Prin urmare, punctul A este o intersecție a două HMT și, prin urmare, detectate.

Clădire. Pe o linie arbitrară MN dintr-un punct arbitrar în amânarea segmentului BC = a. Din orice punct de pe linia MN efectua directă ^ MN FK și FK K din ambele părți concedieze segmente KT și KE ha egale. După T și E efectua n directă și m, perpendicular TE. Din punctul C hold cerc cu raza b.

Intersecția acestei m circumferențiale drepte și n este punctul dorit A. se conecteaza la punctele B și C ale triunghiului ABC - dorit.

Dovada. In triunghiul ABC VS = o bază de construcție, apex A este îndepărtat din partea de jos, la o distanță ha. o parte laterală AC = b.

Studiu. Dacă b> ha. avem patru soluții. pentru că raza unui cerc intersectează liniile m și n în patru puncte.

Dacă b = ha. obținem două soluții, după cum m drept și n va atinge circumferința.

În cazul în care b

a se vedea, de asemenea,

Întâlnire provocările metodei HMT este după cum urmează: A) problema este formulată astfel încât decizia sa vine în jos pentru a găsi piese care îndeplinește una sau mai multe condiții. B) În cazul în care condiția este una, soluția problemei va fi un locus corespunzător. În cazul în care condițiile. [Citește mai mult].