Matematică financiar 2018
Răspunsul este în caractere aldine sau listate la sfârșitul problemei
teste de caz în curs „matematică financiară“
Test1. dobândă simplă
1. Care este principiul disparitate financiare de bani aparținând diferitelor momente de timp?
a) deprecierea de bani din cauza inflației;
b) o creștere a riscului cu creșterea termenului de împrumut;
c) posibilitatea de a investi bani în scopul de a obține venituri;
d) reducerea costurilor de bunuri în legătură cu progresul științific și tehnologic.
2. Precizați căile posibile de măsurare a ratelor dobânzilor
a) Numai la sută;
b) numai fracția zecimală;
c) fracția numai naturală până la 1/32;
g) procente sau fracție zecimală naturale.
3. Introduceți formula pentru simplu interes de compunere.

4. În ceea ce esența practicii franceze de încărcare interes simplu?
a) utilizarea de interes comun și un termen aproximativă a creditului;
b) să folosească procentajul exact și durata aproximativă a împrumutului;
c) să folosească procentajul exact și termenul exactă a creditului;
d) utilizarea de interes comun și termenul exact a împrumutului.
5. În ceea ce este esența practicii germane de încărcare interes simplu?
a) utilizarea de interes comun și un termen aproximativă a creditului;
b) să folosească procentajul exact și durata aproximativă a împrumutului;
c) să folosească procentajul exact și termenul exactă a creditului;
d) utilizarea de interes comun și termenul exact a împrumutului.
6. Care este esența practicii britanice de încărcare interes simplu?
a) utilizarea de interes comun și un termen aproximativă a creditului;
b) să folosească procentajul exact și durata aproximativă a împrumutului;
c) să folosească procentajul exact și termenul exactă a creditului;
d) utilizarea de interes comun și termenul exact a împrumutului.
7. Se specifică formula de calcul a sumei atunci când este aplicat rată atrasă simplu, discret variabile în timp.
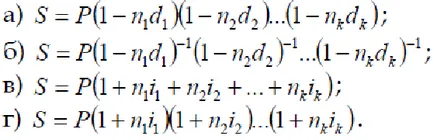
8. Introduceți formula pentru calculul valorii reinvestit în operațiuni atrasă sub variind simplu procente pariu discret.

formulă matematică 9.Ukazhite de actualizare în cazul ratei dobânzii simple.

Formula 10.Ukazhite pentru o rată simplă a dobânzii cont bancar.

Testul 2: Compus interes
1. Introduceți formula prin care se calculează perioada pentru a dubla suma inițială în aplicarea dobânzii compuse.

2. vUkazhite compoundare formula de interes compus.

3. Cum se calculează suma rambleu în aplicarea dobânzii compuse, în cazul în care rata variază în timp discret.
4. Introduceți formula pentru complexul rata de actualizare matematică.

5. Introduceți formula contul bancar al unei rate de actualizare dificilă.
6. Care dintre formulele identifică în mod corect rata dobânzii complexe?
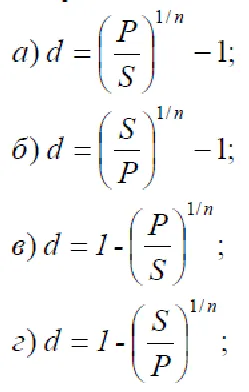
7. Care din formula definește în mod corect un pariu complex?

8. Care dintre formula definește în mod corect o rată a dobânzii nominală complexă?

9. Care este formula reflectă în mod corect relația dintre rata de actualizare nominală de complex și provocator rata anuală de actualizare?

10. Care este formula definește în mod corect puterea de creștere?
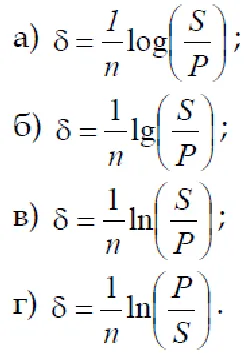
Testul 3. Interesul în contextul inflației și fiscalitate
1. Cum este simplu rata dobânzii r brut pe reale i rata dobânzii și indicele prețurilor Jp?
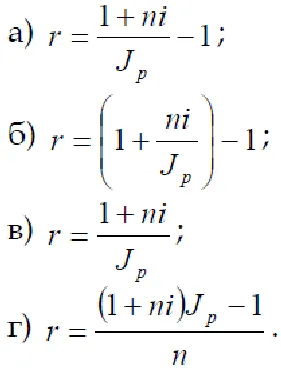
2. Cum este brută - compus rata dobânzii r pe rata reală a dobânzii și inflația i h?
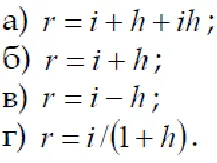
3. Așa cum este definit de prima inflație în calcularea dobânzii simple?
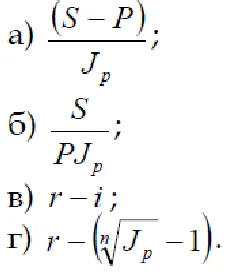
4. Cum este prima inflație în calculul dobânzii compuse?

5. Deoarece rata anuală a inflației (creșterea prețurilor) h asociate cu indicele prețurilor Jp pentru perioada de n?

6. Indicele puterii de cumpărare a banilor este legată de un indice de preț?
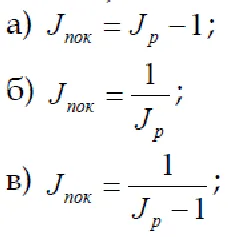
7. Prețul pe trimestru a crescut de 1,2 ori. Orice indice de preț anual corespunzător acest ritm?
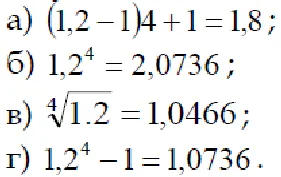
8. Cum este rata reală a dobânzii simple, la rata anuală a inflației h?
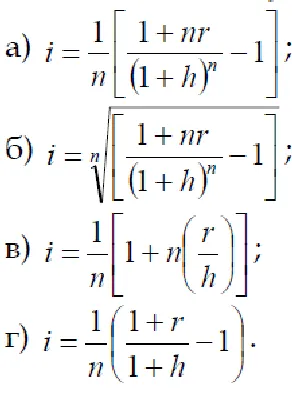
9. Cum este rata reală a dobânzii la rata anuală a inflației h?

Care este taxa pentru anul t în calculul dobânzii compuse, în cazul în care rata de impozitare este egală cu g?

Testul 4. Fluxurile de plată
1. Care este postnumerando chiria?
a) anuitate format în tranșe după un moment specificat;
b) anuităților care primește la sfârșitul fiecărei perioade;
c) chiria, care plățile sunt ajustate pentru inflație;
plăți g) anuităților care sunt ajustate cu valoarea taxei.
2. Care este prenumerando chiria?
a) anuitate formată în rate la unele puncte menționate anterior, în timp;
b) plățile anuitate, care vine de la începutul fiecărei perioade;
c) plata chiriei care vin înainte de ajustare pentru inflație;
plăți g) anuitate care vine înainte de corecție cu valoarea taxei.
3. Care este anuitatea p determinabil?
a) anuitate cu un termen de p ani;
b) anuitate cu o perioadă de calcul interes p ani;
c) chirie plățile către districtul în anul;
g) închiriați de la p acumulate an interes.
4. Care este relația dintre valoarea curentă și acumulate valoarea chiriei?
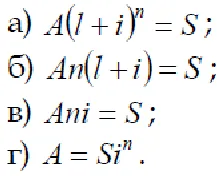
5. Precizați raportul dintre compoundare anuitate convenționale cu o singură sarcină de procente pe an.

6. Se specifică anuitatea ordinară coeficient de reducere cu o singură sarcină de procente pe an.
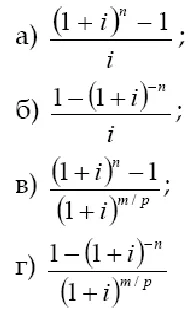
7. Introduceți convențional factorul de compoundare p - anuitatea imediată ca m - ori dobânda acumulată, în cazul general.
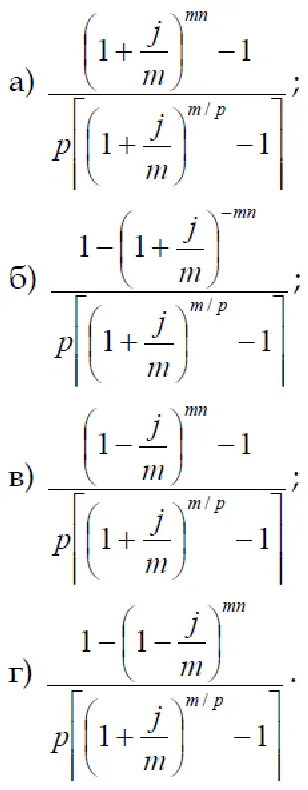
8. Selectați raportul conducere normală p - rentă la m - ori calculul la suta pe an, în general.
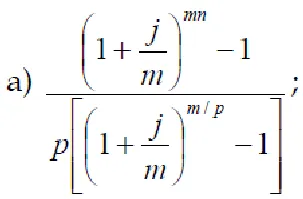
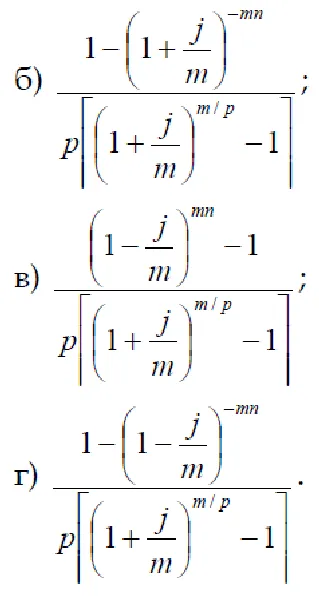
9. Se specifică formula pentru determinarea termenului de o anuitate obișnuită cu o singură sarcină de procente pe an.

10. bUkazhite interpolare liniară formulă.

Testul 5. Aplicarea practică a teoriei
1. Specificați un factor de combinare funcționarea pe termen scurt cu dublu sistem de conversie valutară LES → Frecați. → Frecați. → SLE.
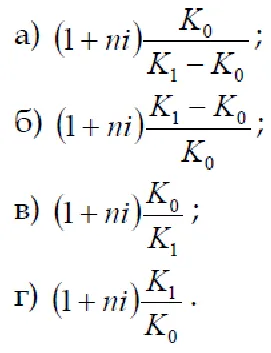
2. Precizați relația funcțională dintre performanța anuală am FEP. funcționarea pe termen scurt cu dublu sistem de conversie LES → Frecați. → Rub. → SCR rata de creștere a ratei de schimb pentru perioada de funcționare k
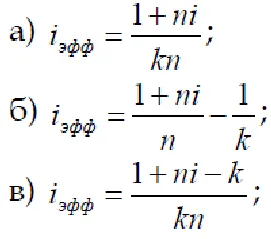
3. Care este valoarea critică a ratei cursurilor de schimb pentru perioada de creștere k operare în care eficiența de funcționare este egală cu zero, în cazul în care acesta este o operațiune pe termen scurt a sistemului de LES → Frecați. → Frecați. → SLE?

4. Care este K1 valoarea maximă admisibilă este rata de schimb de la sfârșitul circuitului operare SCR → Rub. Freca →. → LES, în care depozit pe termen scurt în ruble sau monedă la fel de eficiente.
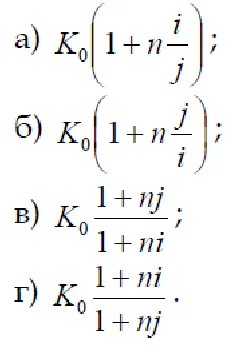
5. Specificați un factor de agravând funcționarea pe termen scurt cu dublu sistem de conversie valutară Frecați. → → SLE LES → Rub.

6. Precizați relația funcțională dintre performanța anuală am FEP. funcționarea pe termen scurt cu dublu sistem de conversie Frecați. → → LES LES → Rub. cu rata de creștere a ratei de schimb în cursul perioadei de funcționare k.
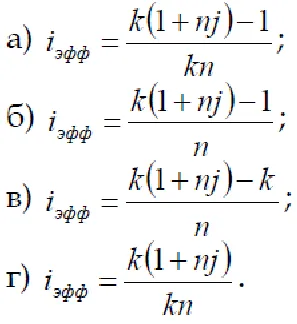
7. Este critic rata de schimb rata k pentru creșterea pe termen operare în care eficiența de funcționare este egală cu zero, în cazul în care discursul scurt
Frecați sistemul de operare. → → SLE LES → Rub.?
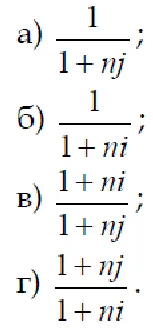
8. este minimă rata admisibilă de schimb valoarea K1 la sfârșitul Frecați circuitului de funcționare. LES → → → Rub LES. în care depozit pe termen scurt în ruble sau valută străină este la fel de eficientă.
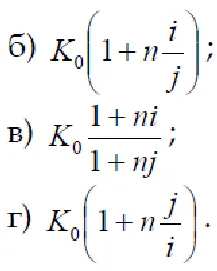
9. acumulate la acea dată În cazul în care rambursarea datoriei pe termen scurt a sumei de plată este mai mică decât suma de interes în metoda actuarială:
a) plata rasplateste partea relevantă din dobânda acumulată și dobânda restul este de a crește valoarea datoriei;
b) plata nu este luată în considerare, și este atașat la plata următoare;
c) plata nu este inclus, dar împreună cu dobânda acumulată pe ea este atașat la plata următoare;
g) transferul nu este considerat la început, dar apoi evaluate împreună cu ea la o rată scăzută (prestabilită) de interes este atașat la următoarea plată.
10. Atunci când fluxurile de numerar în contul curent și calcularea cuantumului dobânzii simple de interes în momentul închiderii contului se calculează astfel:
a) suma procentajului de numere separate printr-un divizor constantă;
b) suma ponderată a procentului de numere, cu greutățile determinate de sumele din contul curent, împărțit printr-un divizor constant;
c) suma ponderată a procentelor de numere, cu greutăți determinate perioade de constanță a sumelor în contul curent împărțit la constanta divizor;
d) suma ponderată a procentului de numere, cu greutățile determinate de produsul sumei contului curent la conturile constanța intervalului în zilele divizate de o divizor constantă.