Informații codificării Rezumat - abstractizeaza lucrări bancare, rapoarte, documente de termen și disertații
2. Codurile de clasificare
3. Metode de coduri de prezentare
Codurile de reprezentare 3.1 Matrix
3.2 Reprezentarea codurilor într-un copac cod
3.3 Prezentarea codurilor sub forma polinoamelor
3.4 Codurile de reprezentare geometrică
1. Codificare. Concepte de bază și definiții
Luați în considerare conceptele de bază legate de codificare de informații. Pentru transmisia sunt convertite în semnale în canalul de comunicație de comunicare. Caracterele cu care pentru a crea un mesaj de forma alfabetul primar, fiecare simbol este caracterizată prin probabilitatea apariției sale într-o declarație. Fiecare mesaj corespunde în mod unic unui semnal care reprezintă o secvență specifică de simboluri discrete elementare numite codewords. Encoding - Acest mesaj de conversie într-un semnal care este conversia mesajelor către codewords. Cod - respectarea între elementele mesajelor de sistem și cuvintele de cod. Encoder - un dispozitiv care efectuează codificare. dispozitiv Dekoder- care efectuează operația inversă, adică conversia unui cuvânt de cod în mesaj. Alfabetul - un set de posibile elemente de cod, și anume Simbolurile elementare (simboluri de cod) X =, unde i = 1, 2. m. Numărul de elemente de cod - m se numește bază. Pentru xi = binary și m = 2. Secvența finală a caracterelor alfabetului se numește cuvânt cod (cod cuvânt). Numărul de elemente într-un cuvânt de cod - n numita valență (combinație lungime). Numărul de diferite codewords (N = mn) se numește un volum sau capacitate de cod.
În cazul în care N0 - numărul sursei, apoi N-am N0. O multitudine de stări de cod trebuie să acopere o multitudine de state ale obiectului. uniforma completa n - cod cifre cu baza conține m N = mn codewords. Un astfel de cod este numit primitiv.
2. Codurile de clasificare
Codurile pot fi clasificate în funcție de diverse criterii:
1. La baza (numărul de caractere din alfabet): binar (m binar = 2) și binar (m № 2).
2. De-a lungul lungimea (cuvintele cuvintele-cod):
uniformă - în cazul în care toate codewords au aceeași lungime;
Neuniforma - în cazul în care lungimea nu este constantă nume de cod.
3. Prin transmiterea metodă care cuprinde:
serial și paralel;
bloc - date este mai întâi tamponată și apoi transferat la canalul binar și continuu.
Imunitatea 4. Zgomot:
simplu (primitiv, plin) - pentru a transmite informații utilizând toate codewords posibile (fără redundanță);
corective (interferențe radio suprimat) - pentru a trimite mesaje nu folosesc toate, ci doar o parte din cuvintele de cod (autorizate).
5. În funcție de scopul și aplicarea următoarelor tipuri de cod condiționale se pot distinge:
Codurile interne - codurile utilizate în interiorul dispozitivului. Acest cod mașină și coduri bazată pe utilizarea sistemelor de poziționare numeral (binar, zecimal, binar codificat zecimal, octal, hexazecimal, etc.). Cel mai frecvent cod într-un calculator este un cod binar, ceea ce îl face ușor de implementat în dispozitive hardware pentru stocarea, procesarea și transmiterea datelor în cod binar. Acesta asigură o fiabilitate ridicată și simplitatea dispozitivului operațiunilor pe date în cod binar. date binare, combinate în grupuri de câte patru pentru a forma un cod hexazecimal, care este în bună concordanță cu arhitectura de calculator, care funcționează cu octet de date multiple (8 biți).
Coduri pentru schimbul de transmitere a datelor prin canalele de comunicare. Utilizate pe scară largă în PC-ul a primit codul ASCII (American Standard Code pentru schimbul de informații). ASCII - este codul de 7 biți de alfanumerice și alte caractere. Deoarece computerele funcționează cu octeți, este bitul opta este utilizat pentru sincronizare sau de paritate, sau cod de dispersie. În computer IBM utilizează un cod extins binar-zecimal codificat pentru schimbul de informații EBCDIC (Extended Binary Coded Decimal Interchange).
Atunci când informația de codificare pentru transmisie peste un canal de comunicație, inclusiv în căile de hardware, codurile sunt utilizate pentru viteza maximă de transfer a datelor datorită eliminării sale de compresie și redundanță (de exemplu, codurile Huffman și Shannon-Fano) și a codurilor pentru asigurarea fiabilității transmisiei de date, prin introducerea redundanță în mesajele transmise (de exemplu, codurile de grup, Hamming, ciclice și variantele lor).
Codurile pentru aplicații speciale - sunt coduri menite să abordeze sarcinile specifice de transmitere și prelucrare a datelor. Exemple de astfel de coduri este gri cod ciclic, care este utilizat pe scară largă în aghiotanți deplasărilor unghiulare și liniare. Codurile Fibonacci sunt utilizate pentru construirea de ADC de mare viteză și de imunitate.
Accentul cursului este dat coduri pentru schimbul de date și transmiterea prin intermediul canalelor de comunicare.
1) Creșterea eficienței transmisiei de date, din cauza ratei maxime de date.
2) Îmbunătățirea imunitate de zgomot în timpul transmisiei de date.
În conformitate cu aceste obiective de codificare teoria dezvoltată în două direcții majore:
1. Teoria economică (optimă eficientă,) de codificare caută coduri care permit canale fără interferențe pentru a crește eficiența de transmitere a informațiilor prin eliminarea redundanță sursa, iar cea mai buna viteza de transmitere a datelor de potrivire de capacitatea canalului de comunicare.
2. Teoria de codificare de corectare a erorilor este în căutarea de coduri care crește fiabilitatea de transmitere a datelor în canalele zgomotoase.
3. Metode de coduri de prezentare
În funcție de metodele de codare aplicate, folosind coduri diferite modele matematice, cel mai des folosit reprezentarea cod sub formă de matrici de cod; copac cod; polinoame; forme geometrice, etc.
Codurile de reprezentare 3.1 Matrix
Este folosit pentru a reprezenta uniform n - codurile numerice. Pentru primitive (complet și uniform) matricea de cod cuprinde n - coloane și 2n - linii, adică cod utilizează o combinație a tuturor. Pentru erori de corectare (reglare, detectarea și corectarea erorilor), matricea cuprinde n - coloane (n = k + m, unde k-numărul de informații și m - numărul de biți de verificare) și 2k - rânduri (unde 2k - numărul de codewords admisibile). Pentru valori mari ale lui n și k matricea va fi prea greoaie, codul este scris în formă prescurtată. O reprezentare matriceală a codului utilizat, de exemplu, un grup de coduri liniare, coduri Hamming, etc.
3.2 Reprezentarea codurilor într-un copac cod
Cod copac - conectat grafic fără cicluri. Grafic conectat - un grafic în care există o cale care leagă aceste noduri în fiecare pereche de noduri. Graficul este format din noduri (vârfuri) și muchiile (sucursale) ce conectează nodurile situate la diferite niveluri. Pentru a construi un arbore binar de uniform vertex selectat numit rădăcina copacului (sursa) și de marginile se realizează în următoarele două vârfuri, etc.
Exemplu cod arbore pentru codul complet este prezentat în figura 1.
1 0 1 0 1 0 1 0
110 101 100 111 011 010 001 000
Fig.1. Arborele un cod binar complet atunci când n = 3
Arborele de cod de corectare a erorilor este construit pe baza unui copac cod complet prin eliminarea combinațiile de cod interzise. grafic ponderată, cu marginile lemnului pentru a indica probabilitatea tranzițiilor este utilizat pentru codul inegale de lemn. Reprezentarea codului sub forma arborelui de cod este folosit, de exemplu, codurile Huffman.
3.3 Prezentarea codurilor sub forma polinoamelor
Reprezentarea sub forma unor coduri polinoame bazate pe similaritate (izomorfism) spațiu n binar - secvențe și spațiul polinoame de grad cel mult n - 1.
Cod pentru orice sistem de numerație cu baza X poate fi reprezentat ca:
G (x) = o-1 xn-1 + o-2 + xn-2. + A1 x + a0 =,
unde ai - figuri ale radix (binare 0 și 1);
x - simbolic (inactiv) exponent variabilă care corespunde cifrelor binare chisla-
De exemplu: 1010110 Cuvântul de cod poate fi reprezentat ca:
G (x) = 1Chx6 0Chx5 + + + 1Chx4 0Chx3 1Chx2 + + + 1Chx1 0Chx0 = x6 + x4 + x2 + x = 10101
În acest caz, funcționarea codurilor sunt operațiuni echivalente pe polinoame. Codurile de prezentare sub formă de polinoame este utilizat de exemplu în coduri ciclice.
3.4 Codurile de reprezentare geometrică
Orice combinație de n - cod binar biți poate fi reprezentat ca un n vertex - unitate dimensional cub, adică cub cu lungimea muchiei egală cu 1. Pentru cod de două elemente (n = 2) codewords sunt aranjate într-un pătrat noduri. Pentru codul de trei elemente
(N = 3) - la nodurile unei unități cub (Figura 2).
În general, n cub are vârfuri -dimensional 2n care corespunde unui set de combinații de cod 2n.
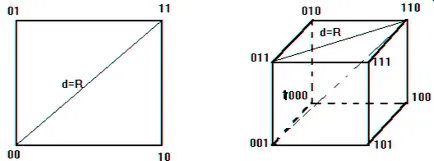
Fig.2. Modelul geometrica cod binar
Interpretarea geometrică a distanței de cod. Codul distanță - numărul minim de muchii care trebuie să fie traversate pentru a obține de la un cuvânt de cod la altul. distanța Cod caracterizează codul de corectare a erorilor.
Klovsky DD semnalizare teorie. -M. Comunicare 1984.
Dmitriev VI Teoria informației aplicată. M. Școala Superioară din 1989.