geometrie E-curs pe secțiuni de construcție poliedrelor

Tipul lecției: lecție combinată.

Scopuri și obiective.

• Formarea obrazovatelnaya- și dezvoltarea reprezentărilor spațiale ale studenților; dezvolte abilități de rezolvare a problemelor pentru a construi secțiuni ale simple poliedre;
• vospitatelnaya- educa voința și perseverența de a obține rezultatele finale în construcția unor tronsoane din cele mai simple poliedre; cultiva dragostea și interesul pentru studiul matematicii.
• Dezvoltarea razvivayuschaya- a gândirii logice în elevi, concepte spațiale, dezvoltarea abilităților de auto-management.

Echipamente. calculatoare cu un program special conceput, diapozitive imprimate sub formă de desene finisate cu obiectivele corpului poliedre, carduri individuale cu temele.

Structura lecție.

1. Subiecte post și obiectivele sesiunii (2 minute).
2. Instruindu pentru a efectua sarcini pe computer (2 min).
3. Actualizarea cunoștințelor de referință și a abilităților elevilor (4 min).
4. Testarea cu auto-test (3 minute).
5. Rezolvarea problemelor cu un profesor care explică progresul soluției (15 min).
6. Munca independentă cu auto-test (10 min).
7. Formularea temelor (2 min).
8. Rezumarea (2 min).

1. subiectul mesajului și obiectivele lecției

După verificarea disponibilității de clasă la o lecție profesorul a spus că a avut loc astăzi o lecție pe tema „secțiuni de construcții de poliedre“, va aborda problema în construcția de secțiuni ale unora dintre cele mai simple avioane poliedre care trec prin cele trei puncte care aparțin marginile poliedre. Lecția va fi folosind o prezentare calculator realizată în Power Point.

2. Instrucțiuni privind siguranța la locul de muncă în laboratorul de informatică

Profesor. Vă atrag atenția asupra faptului că începe să lucreze în laboratorul de informatică, și trebuie să respecte regulile și să lucreze la calculator. Fixați partea de sus de masă de alunecare și să urmeze aterizare corectă.

3. Actualizarea de referință a cunoștințelor și abilităților elevilor

Profesor. Pentru a rezolva multe probleme asociate cu poliedre geometrice, este util să fie în măsură să se bazeze pe secțiunea lor sub diferite planuri, pentru a găsi punctul de intersecție al liniei drepte a planului, găsi intersecția a două planuri de date. În lecțiile anterioare am analizat secțiuni ale avioanelor poliedre paralele cu marginile și fețele poliedrului. În această lecție ne vom uita la problema în construcția de secțiuni ale planului care trece prin cele trei puncte de pe marginea poliedru. Pentru aceasta considerăm cea mai simplă poliedre. Care sunt aceste polihedre? (Prezintă un model cub de tetraedru, piramida patrulateră regulată, o linie de prisme triunghiulare).

Elevii ar trebui să determine tipul de poliedru.

Profesor. Să vedem cum arată pe ecran. De la o imagine la alta miscare prin apăsarea butonului din stânga al mouse-ului.

Pe ecran una după alta imagine numită poliedre.

Profesor. Reamintim că se numește o secțiune a poliedru.

Student. Poligon ale cărui laturi sunt segmentele care aparțin fețele poliedrului, capetele pe marginile unui poliedru, rezultat intersecția polyhedron planul de tăiere arbitrar.

Profesor. Ceea ce poligoanele pot fi secțiuni de date poliedre.

Student. cub intermediară: trei - șase pătrate. triunghiuri tetraedru sectionale, patrulatere. Secțiunile transversale ale unei piramide patrulater si prisme triunghiulare: trei - cinci pătrate.

4. Testarea unei auto-verificare

Profesor. În conformitate cu conceptul de secțiuni de poliedre, cunoștințe solide geometrie axiome și dispunerea liniilor și avioane în spațiu, sunteți invitați să răspundă la întrebările de testare. Computer apreciați. Punctaj maxim 3 puncte - 3 răspunsuri corecte. Pe fiecare diapozitiv, faceți clic pe butonul cu numărul de răspunsul corect. Lucrezi în perechi, astfel încât fiecare dintre voi va obține aceleași, scorurile de calculator. Faceți clic muta cursorul la următorul diapozitiv. La executarea de muncă se administrează timp de 3 minute.

I. Care figură prezintă o secțiune a unui cub ABC avion?

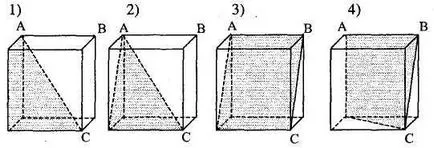
II. La care figura prezintă o secțiune transversală în plan a piramidei prin diagonală BD de bază paralelă cu marginea SA?

III. La ce figura arată secțiunea tetraedru care trece prin punctul M paralel cu planul ABS?

5. Rezolvarea problemelor cu explicarea soluțiilor de curs profesorilor

Profesor. Mai departe direct la rezolvarea problemelor. Faceți clic muta cursorul la următorul diapozitiv.

Sarcina 1 Această sarcină va lua în considerare orală pas care arată construcția ecranului monitorului. Tranziția se realizează făcând clic pe mouse-ul.

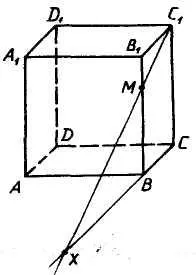
Profesor. Căutând punctul X aparține unui C1 M drept, și, prin urmare, VV1S1 avionul. Care este poziția relativă a avioanelor VV1S1 și ABC.

Student. Aceste planuri se intersectează într-o linie dreaptă BC.

Profesor. Deci, toate punctele comune VV1S1 și avioane ABC fac parte din linia BC. Căutând punctul X trebuie să aparțină ambelor planuri de două fețe: ABCD și BB1C1C; rezultă că punctul X trebuie să se afle pe linia de intersecție, adică. e. pe linia BC. Prin urmare, punctul X ar trebui să revină simultan în două linii: S1M și VS și, prin urmare, este punctul lor de intersecție. Construcția punctului dorit, ia în considerare ecranul monitorului. Secvența de a construi veți vedea la clic pe butonul stâng al mouse-ului: S1M si BC continua sa se intersectează în punctul X. care este punctul necesar de intersecție cu planul drept S1M punctul de a ABCD.

Profesor. Pentru a trece la următoarea sarcină, utilizați cursorul pentru a trece la următorul slide. Această problemă este considerată o prescurtare pentru constructii.

a) construi cub plan secțiune care trece prin punctul A1. MD1C1 și NDD1 și b) Găsiți intersecția planului de tăiere cu planul bazei inferioare a cubului.

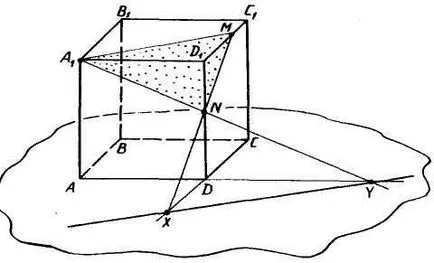
Decizie. I. planul secant este o fațetă A1B1C1D1 două puncte comune A1 și M, și, prin urmare, se intersectează cu ea într-o linie dreaptă care trece prin aceste puncte. puncte Conectarea segmentului A1 și M a liniei, găsi intersecția următoarea secțiune a planului și planul feței superioare. Acest fapt va fi scris după cum urmează: A1M. Apăsați butonul din stânga al mouse-ului, apăsarea va fi construit acest drept.

În mod similar, vom găsi linia de intersecție cu planul care se intersectează fețele și AA1D1D DD1S1S. Prin apăsarea butonului mouse-ului, veți vedea un raport de sinteză și progresul de construcție.

Astfel A1NM. secțiunea transversală dorită.

Ne întoarcem acum la a doua parte a problemei. Noi găsim linia de intersecție a planului de tăiere cu planul bazei inferioare a cubului.

II. Secantă plan cu planul de bază al cubului intersectează o linie dreaptă. Pentru a portretiza suficient de directă pentru a găsi două puncte aparținând liniei de date, de ex punctul general, planul de tăiere și planul de ABCD feței. Bazat pe sarcini anterioare vor fi astfel puncte: punctul X =. Apăsați butonul, veți vedea un rezumat de înregistrare și de construcție. Și punctul Y. crezi, băieți, cum să-l?

Profesor. Uită-te la ecranul de clădirea ei. Faceți clic pe butonul mouse-ului. Conectarea punctele X și Y (Record X -Y), obținem linia dreaptă dorită - linia de intersecție cu planul care intersectează planul bazei inferioare a cubului. Faceți clic pe butonul stâng al mouse-ului - stenografie si constructii.

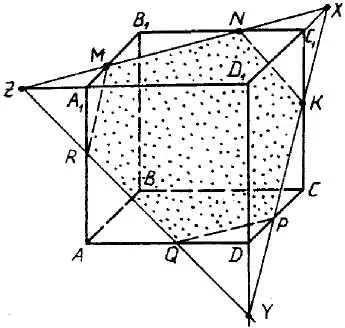
Activitatea 3 Construct cub plan secțiune care trece prin punctele:

Doar apăsând butonul mouse-ului, veți vedea pe monitor progresul de construcție și o înregistrare scurtă. Bazat pe conceptul secțiunii transversale, găsim suficient în planul fiecărei fețe două puncte pentru a crea o linie de intersecție a planului de tăiere și planul de fiecare față a cubului. Punctele M și N aparțin plane A1V1S1. Prin combinarea lor, vom obține o linie de intersecție a planului de tăiere și fața superioară a planului cub (apăsați butonul mouse-ului). Continuă MN drept și D1C1 înainte de a traversa. H. obține un punct aparținând atât planul A1V1S1. și DD1C1 plan (click). Punctele N și K aparțin plane VV1S1. Prin combinarea lor, obținem linia de intersecție planul de tăiere și se confruntă cu VV1S1S. (Mouse clicuri). Conectarea punctelor X și K, și continuați drept până la intersecția cu linia HC DC. Obținem punctul P și lungimea CD - linia de intersecție de tăiere plan și se confruntă cu DD1C1C. (Mouse clicuri). Continuați direct pe CD-ul și DD1 până la intersecția, obținem punctul Y aparținând AA1D1 plan. (Mouse clicuri). În planul acestei feței, avem nevoie de mai mult de un punct, pe care o primim ca urmare intersecție a liniilor MN și A1D1. Acesta este punctul. (Mouse clicuri). Și conectarea punctelor Y și Z. obține. (Mouse clicuri). Combinând Q și R, și R. M. obține? secțiunea transversală dorită.

Scurt record de construcție: