filtre lowpass

.

În passband, adică pe intervalul de la 0 la

pătrat Cebîșev polinom va varia în intervalul [0; 1], luând alternativ valorile extreme (n + 1) ori. Funcția și intervalul de frecvență considerat va primi același număr de ori valorile [0; 916 #; a].

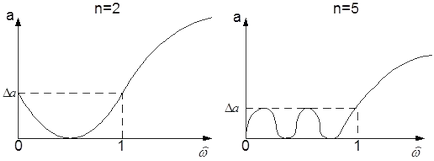
Figura 6 prezintă grafice de amortizare Cebîșev polinomiale LPF pentru valorile n = 2 și n = 5 pentru identice # 916; a.

teste funcționale și (

) Vă permite să facă o serie de concluzii importante și interesante pentru practica:

1. Cu una și aceeași valoare a # 916, și de a crește ordinea funcției de transfer crește prăvăliș caracteristici de atenuare în afara passband.

2. Cu o valoare constantă de lățime de bandă n atenuare este mai mare, cu atât mai mare # 916; a.

3. Cel mai mic (egal cu 0) și cea mai mare (egal # 916; a) atenuare valori alternative în passband. „Egale pe dimensiuni“ Acesta este motivul pentru apropierea Cebîșev adesea numit.

4. Atenuarea filtrului la arestarea banda cu creșterea crește frecvența monoton.

Conform specifica cerințele pentru atenuarea caracteristică în ordine stopband Cebîșev filtru lowpass se calculează în același mod ca și comanda Butterworth filtru trece jos, pornind de la starea A (

)

Rezolvarea această inegalitate pentru n obținem:

Construcția funcției T (p) este cunoscut | T (j

) | 2 este produs în mod obișnuit. punerea în aplicare a schemei scara va avea aceeași formă ca și cea a oricărui alt polinom filtru low-pass cu aceeași n.

Diferența este doar în valorile valorile parametrilor elementelor. soluții tabelate pentru calcularea Cebîșev LPF dat în literatura de referință.

filtru Cebîșev are avantajul că același număr de elemente și în același timp, # 916: și o bandă de trecere, filtrul are o atenuare mai mare în comparație cu banda oprită filtru Butterworth.

3. LPF cu amortizare rafale (f-ry Zolotareva)

O trăsătură distinctivă a caracteristicilor de amortizare ale LPF este un polinom de o creștere monotonă, cu creșterea distanței de la passband. Cu toate acestea, dacă doriți să sintetizeze un LPF cu un nivel semnificativ de A0 atenuare garantată și o bandă de tranziție îngustă, utilizarea structurilor polinomiale conduce la număr nejustificat de mare de elemente în astfel de cazuri, este logic să apeleze la alte funcții de transfer, în special, au zerouri, și stropi banda de detenție degradare, adică funcțiile de forma:

- Hurwitz polinom de gradul n;

- bandă de reținere frecvență în cazul în care răspunsul în frecvență al filtrului devine zero (atenuare devine infinit de mare, adică deține ei „explozie“).

Dependența de frecvență a atenuării este:

Printre filtrul low-pass, a cărei funcție de transfer în formă fracția (5), cele mai utilizate pe scară largă filtru low-pass cu caracteristici de atenuare izoekstremalnymi Zolotaryova sau LPF.

Cerințe pentru caracteristica de amortizare LPF a acestui tip este formulat după cum urmează: atenuarea în banda de trecere a filtrului nu trebuie să depășească o valoare prestabilită # 916; o și bandă de reținere să nu fie mai mică decât o valoare predeterminată a0.

In astfel de cazuri, filtrul de aproximare cu caracteristicile de atenuare a sarcinilor folosind una dintre cele mai bune funcții de aproximare formulate și soluționate EI Zolotarev (1847-1878), profesor la Universitatea din St. Petersburg, un elev PL Cebîșev, și anume problema unei funcții raționale de ordinul n, valorile a căror valoare absolută în intervalul -1

1 nu ar fi mai mare decât unul, și în intervalul |

|> 1 cea mai mică în valoare absolută, valoarea ei ar fi cel mai bun posibil.

Funcția rațională adecvată poate fi numită fracție Zolotaryova.

Dacă expresia a = 10lg (1 + A0 Pn 2 (

) Fracția Zolotaryova înțeleasă, în conformitate cu proprietățile valorii finale a celei mai mici atenuare a filtrului în banda de reținere este cea mai mare posibilă în comparație cu toate celelalte filtre cu aceleași valori.

Programeaza caracteristici de atenuare LPF Zolotaryova, și, de asemenea, sunt prezentate posibile de implementare a circuitului pentru cazul n = 5 în figura 7.

Se observă că vârfurile de atenuare sunt aranjate astfel încât valoarea minimă în banda de reținere sunt identice și egale.

Filtre cu caracteristici Zolotaryova (sau pur și simplu Zolotaryova LPF), uneori numite eliptice, deoarece valorile de zero-uri și poli fracțiune Zolotaryova exprimate în ceea ce privește funcțiile eliptic.

Deciziile referitoare la calculul LPF Zolotaryova intabulat în prezent și a adus la circuitele și valorile parametrilor elementelor (vezi. L.2, pp. 292-295).

Eficacitatea Zolotaryova LPF poate fi confirmată printr-un exemplu în care un filtru low-pass impune cerințe mai degrabă stricte.

Calculul de ordinul n diferite filtre care îndeplinesc cerințele de mai sus va duce la:

Numărul de elemente egal cu, respectiv, 7, 18, 80.

În acest exemplu, LPF Zolotarev este în mod clar în afara competiției.

Studiu detaliat al proprietăților diferitelor filtre poate concluziona că, în anumite cazuri particulare, cu o benzi de tranziție relativ largi numărul minim de elemente pot avea un LPF polinom. Pot exista situații în care numărul de elemente Zolotaryova LPF si LPF Cebîșev polinomial sunt identice. Apoi, se preferă un tip care este mai mult pe deplin îndeplinește celelalte cerințe (dimensiune, tehnologia de producție, etc.).

Literatura folosită pentru prepararea prelegerile

1. AF Beletsky „Teoria circuitelor electrice liniare» 1986 Bucuresti c 368-395

Toate materialele din „Telecom“