figura
1 Mecanică 1 Cinematica mișcării de translație și de mișcare de rotație a punctului
viteză punct egal cu derivata prima dată a vectorului rază.
Viteza medie a punctului se deplasează spre punctul de la intervalul de timp în care se face mișcarea.
Punct de accelerare este egal cu derivata prima dată a vitezei.
Accelerația poate fi reprezentat ca suma componenta tangențială și normală, unde S - natural de coordonate, ρ - raza de curbură a punctului traiectorie, - viteza tangențială.
punct de mișcare, la o viteză constantă () :.
Propunerea unui punct cu o accelerație constantă () ,,,.
Deplasarea punctelor cu accelerație tangențială constantă () :.
punct de mișcare cu o viteză unghiulară constantă ().
modul de comunicare viteza unghiulară ω cu frecvența de rotație ν. .
Comunicare unghiul de rotație φ - φ0 cu numărul de rotații N ..
Accelerația unghiulară este egală cu derivata prima dată a vitezei unghiulare.
Propunerea unui punct cu o accelerație unghiulară constantă ().
Legătura dintre cantitățile unghiulare și liniare: în cazul în care.
Viteza și accelerația la cazul general de mișcare:
legea plus viteză :.
Legea de adăugare de accelerații.
Punct de material M se deplasează cu o viteză de circumferință. Fig. 1 prezintă un grafic de proiecție skorostiot timpului (- vector unitate în direcția pozitivă - este direcția proektsiyana). Vectorul de accelerare completă în Fig. 2 are direcția ...
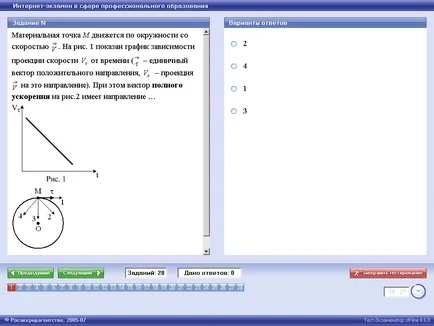

În metoda naturală de a lua în considerare accelerarea punctului. Graficul arată că frânele punctul M (cu creșterea timpului scade). accelerația tangențială este îndreptată în direcția opusă vectorului de viteză (în figura 1, se observă că ;.). pentru că mișcare curbilinie, accelerația centripetă (R - raza cercului din figura 2.) este nenul și este direcționat de-a lungul traiectoriei normale a centrului de curbură, care coincide cu direcția 3 în Fig.2. accelerație maximă. Conform cifrelor arată că această tendință 4. Răspuns: 2
Punct de material M se deplasează cu o viteză de circumferință. Fig. 1 prezintă un grafic de proiecție skorostiot timpului (- vector unitate în direcția pozitivă - este direcția proektsiyana).
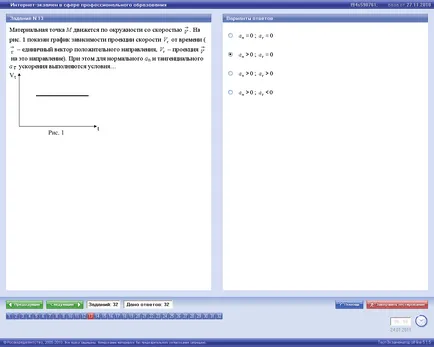
În acest caz, sunt îndeplinite condițiile pentru accelerația normală și tangențială ...
Punctul M spirale cu viteză constantă în direcția indicată de săgeată. Valoarea accelerației totale ...
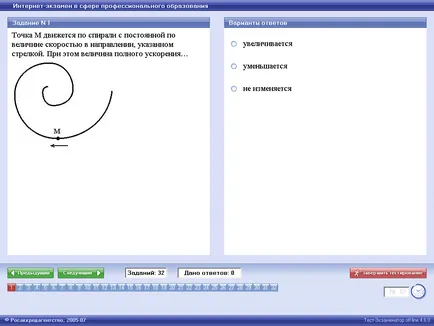
3. neschimbat
accelerație maximă. tangențiale de accelerare caracterizează viteza de schimbare a vitezei magnitudine :. Deoarece modulul constanta vitezei și condiția, valoarea (mișcare uniformă). accelerație normală caracterizează viteza de schimbare a direcției vitezei :. pentru că ca și punctul M de-a lungul unui traseu în spirală scade raza de curbură R (vezi. figura), și modulul vitezei constante, crescând apoi. Prin urmare, amploarea deplină a accelerației crește. Răspuns: 1
Punctul M spirale cu viteză constantă în direcția indicată de săgeată. Valoarea accelerației normale ...
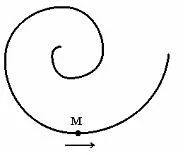
3: Nu sa schimbat
accelerație normală caracterizează viteza de schimbare a direcției vitezei :. pentru că ca și punctul M de-a lungul o rază spirală traiectorie de curbură crește p (vezi. fig.), iar starea modulului de viteză constantă, apoi scade. Răspuns: 1
Punctul M se deplasează în spirală în direcția indicată de săgeată. accelerația normală a velichinene schimbat. În acest caz, viteza este ...
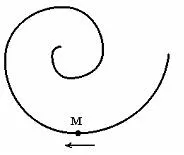
3: Nu sa schimbat
accelerație normală caracterizează viteza de schimbare a direcției vitezei :. Aici. Prin ipoteză, cifra arată că, odată cu mișcarea punctului M măsurată pe o rază de curbură traseu în spirală ρ scade. Astfel, viteza scade. Răspuns: 1
Punctul M se deplasează în spirală în direcția indicată de săgeată. accelerația normală a velichinene schimbat. În acest caz, viteza este ...

3: Nu sa schimbat
accelerație normală caracterizează viteza de schimbare a direcției vitezei :. Aici. Prin ipoteză și din figură se vede că ca punctul M de-a lungul o rază spirală traiectorie a crește curbura p. Prin urmare, viteza crește. Răspuns: 1
Punctul M spirale cu viteză constantă în direcția indicată de săgeată. Valoarea accelerației totale ...
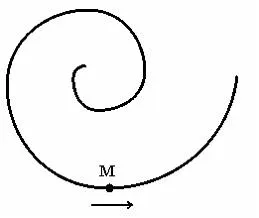
3: Nu sa schimbat
accelerație maximă. tangențiale de accelerare caracterizează viteza de schimbare a vitezei magnitudine :. Deoarece modulul constanta vitezei și condiția, valoarea (mișcare uniformă). accelerație normală caracterizează viteza de schimbare a direcției vitezei :. pentru că raza de curbură ρ traiectoriei ca punctul M de-a lungul crește spirala (vezi. figura), iar viteza constantă modulul, apoi scade. Prin urmare, scade plin de accelerare. Răspuns: 1
Punctul M se mută într-o spirală cu o valoare constantă a accelerației normale în direcția indicată de săgeată. Proiecția pe direcția vitezei tangențiale de accelerare ...
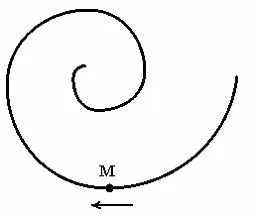
Proiecția accelerației tangențială a axului :. Deoarece proiecția este necesară pentru a determina accelerația tangențială în direcția vitezei, vom alege direcția vectorului unitate coincide cu direcția vitezei atingere, atunci. accelerație normală. Conform problemei: mișcarea punctului M măsurată pe o rază de spirală traiectorie ρ curbură este redusă, prin urmare, de asemenea, ar trebui să scadă valoarea. Prin urmare. Răspuns: 1
Punctul M se mută într-o spirală cu o valoare constantă a accelerației normale în direcția indicată de săgeată. Proiecția pe direcția vitezei tangențiale de accelerare ...

punct material se deplasează cu o viteză constantă de-a lungul celei mai mari curba plan. accelerație ei complet posibil ...
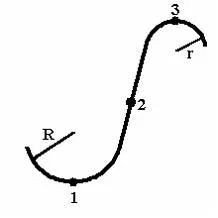
1: 3 până la t * traiectorie.
2 :. R 1 în traiectoria
3 :. 2 t în calea
accelerație maximă. Prin ipoteză, prin urmare. În consecință ,. Prin definiție. La punctul 1, punctul 2, la punctul 3. R în mod inutil> r. atunci. În consecință, accelerația a3 totală> a1> a2. Astfel, maxim A3. Răspuns: 1
Corpul se mișcă cu o accelerație constantă traiectorie normală prezentată în Figura
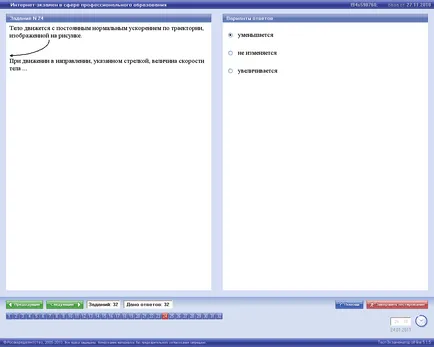
Atunci când se deplasează în direcția indicată de o săgeată, magnitudinea vitezei corpului ...
2: nu sa schimbat
Corpul se mișcă cu o viteză constantă de-a lungul unui arc de cerc care trece într-o linie dreaptă, așa cum se arată în Fig.
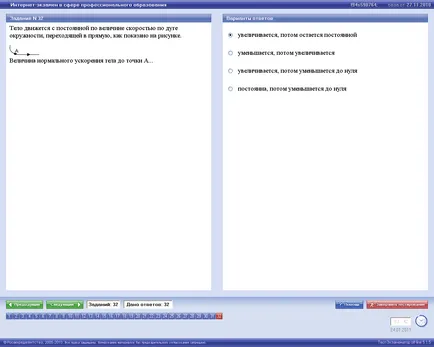
Valoarea accelerației normale a corpului la un punct A ...
1: crește și apoi rămâne constantă *
2: scăderi apoi crește
3: crește, apoi scade la zero
4: constant, apoi scade la zero
Eslii- componentele tangențiale și normale de accelerare, relația: valabil pentru ...
1. mișcare uniformă circumferențial
2. rectilinie uniform accelerată mișcare
3. mișcarea curbilinie uniformă
4. Mișcarea rectilinie uniformă *
Deoarece traiectoria razei de curbură care p = 0: mișcare rectilinie. Deoarece viteza modulului: mișcarea este uniformă. Răspuns: 4
Eslii- componentele tangențiale și normale de accelerare, relația: valabil pentru ...
1: rectilinie mișcare uniform accelerată *
2: o mișcare uniformă rectilinie
3: mișcarea circulară uniformă
4: mișcarea curbilinie uniformă
Deoarece raza de curbură a traiectoriei ρ = ∞: mișcarea rectilinie. Deoarece: uniform accelerată mișcare. Răspuns: 1
Eslii- componentele tangențiale și normale de accelerare, relația: valabil pentru ...
1: mișcarea circulară uniformă *
2: rectilinie mișcare uniform accelerată
3: o mișcare uniformă rectilinie
4: mișcarea curbilinie uniformă
Deoarece viteza modulului: mișcarea este uniformă. Deoarece raza de curbură a traiectoriei ρ = const. mișcare circulară. Răspuns: 1
Eslii- componentele tangențiale și normale de accelerare, atunci mișcarea circulară uniformă următoarele relații:
Accelerarea unei particule se deplasează de-a lungul circumferinței. Modulul tangențiale de accelerare. accelerație normală. Deoarece particula se mișcă cu accelerația unghiulară constantă, viteza unghiulară a ecuației este adevărată. Cu condiția în starea inițială a unei particule în repaus, și, prin urmare ,. La momentul t1 = 1 c. Apoi, accelerația în momentul t1 egal. Ca urmare, raportul dintre normal la accelerare tangent la momentul t1 se determină prin formula (evident că răspunsul la întrebarea specificată în valoare condiție R = 1 m este impar). După înlocuirea valorilor numerice primite. Răspuns: 2
O piatră aruncată la un unghi la orizont, cu o viteză de V. traiectoria într-un câmp gravitațional uniform este prezentat în figură. nici o rezistență a aerului.
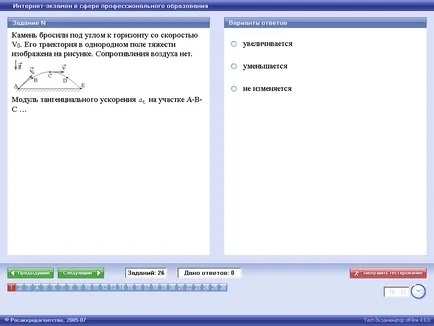
Modulul secțiunea uskoreniyana tangentiala A-B-C ...
3. neschimbat
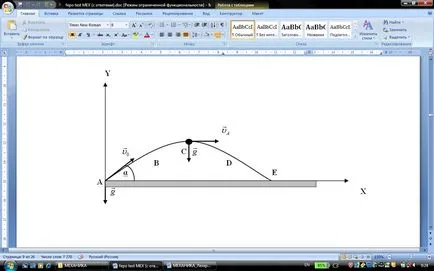

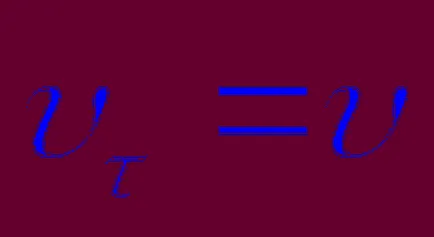
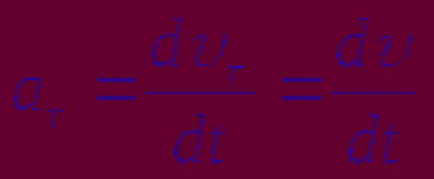
Apoi, viteza modulului în ceea ce privește (1) avem:
Folosind această relație găsim o expresie pentru proiecția accelerației tangențială:
. Pentru modulul accelerare tangențială obține. (2)
Cantitate. In regiunea A-B-C otdo modulul de viteză scade. Prin urmare, pornind de la (2) Modul de accelerație tangențial la secțiunea A-B-C va scădea. Răspuns: 2
O piatră aruncată la un unghi la orizont, cu o viteză de V. traiectoria într-un câmp gravitațional uniform este prezentat în figură. nici o rezistență a aerului.

secțiunea accelerare tangent A-B-C ...
O piatră aruncată la un unghi la orizont cu skorostyuV0. traiectoria într-un câmp gravitațional uniform este prezentat în figură. nici o rezistență a aerului.
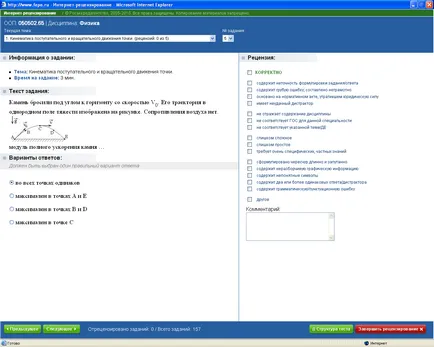
accelerație maximă modul de piatra ...
1.During toate punctele de aceeași
2.maksimalen la punctele A și E
4.maksimalen în tochkahC
relație unghiulară skorostiotvremeni definită de ecuația = 2AT + 5Bt4 (A = 2 rad / s2 și B = 1 rad / c5). Determinarea polnoeuskorenie. line Proektsiivektorovskorostinaetu module viteze egale. Ei iau în considerare semnele de direcție: pozitiv.
și este axa suma proektsiyvektorovnaetu (proektsiina perpendicular pe această direcție axă se compensează reciproc). B. accelerația protonului este. dependența modulului skorostiotvremenipri mișcare ravnozamedlennom este dat. atunci când.
a-1, b = 1 la 2. Care este natura acestui organism? Construiți grafikizavisimosti viteza unghiulară și uskoreniyaotvremeni unghiulară. Amplitudinea mișcării oscilante.
la 73,58%. Când este deschis rezultat pozitiv o intervenție chirurgicală a fost atins în 92.16%, tratamentul prietom. (Tabelul 3).. Grafikzavisimosti gasit taninul este reprezentata de masa probei Naris 1. Valoarea calculată.
cu viteză; care rezultă curba dă poziția x „și y“ ca funcție de t. Curba Uskorenienaetoy va determina câmpul electric în zavisimostiot.