Estimările punct al speranța matematică

SUBIECT: Estimările punctuale ale așteptărilor. Punctul de estimare a varianței. Punctul estimare a probabilității de evenimente. Estimarea punctuală a distribuției uniforme a parametrilor.

estimare p.1.Tochechnye a așteptărilor.

Să presupunem că funcția de distribuție a variabilei aleatoare ξ depinde de parametrul θ necunoscut. P (ξ 0 deține

Astfel, odată cu creșterea mărimii eșantionului crește precizia rezultatului.

Să x1, x2 ... xn - un eșantion de populație care corespunde ξ variabilei aleatoare cu medie necunoscută și o variație cunoscută Dξ = σ 2. realizează mai multe estimări ale parametrilor necunoscute. În cazul în care. ceva care este Evaluarea ia în considerare este o estimare imparțială. Dar, pentru că valoarea nu depinde de mărimea eșantionului n, estimarea nu este consecventă.

Evaluarea efectivă a așteptărilor variabilei aleatoare distribuite în mod normal, este de a evalua

Continuă să evalueze neivestnogo așteptarea unei variabile aleatoare va folosi înseamnă proba, t. E.

Există metode standard (regulate) pentru a obține estimări ale parametrilor necunoscuți ai distribuției. Cele mai cunoscute sunt: ​​metoda momentelor. metoda probabilității maxime și metoda celor mai mici pătrate.

Revendicați estimarea varianței 2 Spot.

Σ 2 variația variabilei aleatoare ξ poate oferi următoarea evaluare:

în cazul în care - înseamnă proba.

Este dovedit faptul că această estimare este bogat, dar mutat.

Ca estimare imparțială consecventă a variației valorii forma un ispol'uet

Este o estimare imparțială a s2, datorită utilizării sale în creștere ca o estimare a valorii Dξ.

Rețineți că în Mathcad oferă o valoare de estimare a varianței în loc s 2. funcția var (x) calculează valoarea

Get-off estimări imparțiale speranța matematică, Danemarca Μξ și variația variabilei aleatoare ξ Dξ pentru o anumită sarcină valori eșantion.

Procedura pentru atribuirea

Citește dintr-un fișier pe disc care conține valorile de probă, sau introduceți valoarea eșantionului de la tastatură.

EXEMPLU quest

Get-off estimări imparțiale speranța matematică, Danemarca Μξ și variația variabilei aleatoare ξ Dξ de valori de exemplu specificați tabelul de mai jos.

Pentru probele din tabel specificat tipul (având în vedere valoarea eșantionului și un număr care indică de câte ori această valoare se găsește în eșantion), formula pentru estimări imparțiale bogate așteptările și varianța sunt de forma:

Document de lucru Fragment estimările Mathcad și calculele sunt prezentate mai jos.

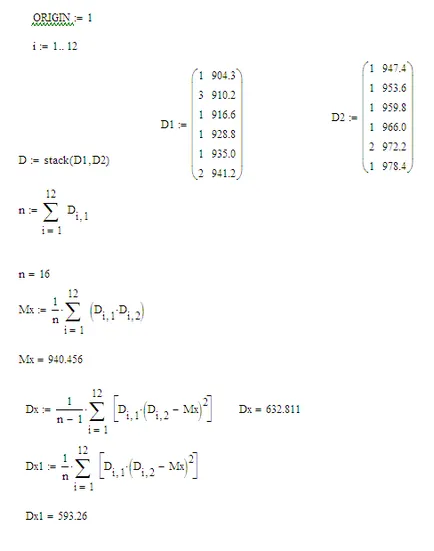
Din calculele de mai sus reiese clar că estimarea părtinitoare dă o valoare scăzută pentru evaluarea dispersiei.

Revendicarea 3. Estimarea punctuală a probabilității evenimentelor

Să presupunem că, în unele experimente evenimentului A (rezultat favorabil al testului-ny) are loc cu o probabilitate p și nu se produce cu probabilitatea q = 1, p. Obiectivul este de a obține estimări de distribuție p necunoscutele parametru-picior pe baza rezultatelor din seria aleatoare de n experimente. Pentru un anumit număr de studii numărul n m gopriyatnyh bla rezultate într-o serie de teste - o variabilă aleatoare, având o distribuție Bernoulli. Am nota cu litera μ.

În cazul în care evenimentul A într-o serie de studii independente n au avut loc

ori m estimarea p propuse calculat prin formula

Clarificarea proprietățile estimării propuse. Din cauza aleator masca are o distribuție Bernoulli μ, apoi Μμ = npiM = M = p. și anume există o estimare imparțială.

Pentru teorema lui Bernoulli un test valabil lui Bernoulli, potrivit căreia, adică Evaluarea p bogat.

Este dovedit faptul că această estimare este eficientă, ca și ceteris paribus minimă varianță.

In Mathcad pentru modelarea valorilor eșantion ale random măști având o distribuție Bernoulli este o rbinom funcție (fc, η, ρ), care generează numere aleatoare vector IZK, dintre care κα-ι zhdoe este egală cu numărul de succese într-o serie de η stagiar independente, tany ρ cu probabilitatea de succes în fiecare.

Simula unele valori eșantion ale variabilei aleatoare, având o distribuție ghidaj Bernoulli cu o valoare predeterminată a parametrului p. Calculeaza pentru fiecare parametru de evaluare probă p și compara cu valoarea-date. Calculul grafic rezultatele prezent.

Procedura pentru atribuirea

1. Utilizarea rbinom caracteristica (1, n, p), descrie și forma-cho secvență variabilă aleatoare, având o distribuție-ghid Bernoulli cu p dată și n pentru n = 10, 20. Ν, în funcție de mărimea eșantionului n.

2. Se calculează pentru fiecare valoare a lui n dot-probabilitate estimarea yatnosti p.

EXEMPLU quest

Punct EXEMPLU count probei de volum n = 10, 200 20 μ variabilă aleatoare, având o distribuție Bernoulli cu parametrul p = 0,3, mai jos.

Notă. Deoarece valoarea funcției este vectorul, numărul de succese într-o serie de studii independente n cu probabilitatea de succes p în fiecare test de conținut în primul component al vectorului rbinom (1, n, p). și anume numărul de succese este rbinom egal (1, n, p). În fragmentul de mai sus componenta k- lea a vectorului p conține un număr de succese într-o serie de studii independente 10k pentru k = 1,2. 200.

n. 4. Parametrii estimare punctuală distribuție uniformă

Referindu-se la încă un alt exemplu instructiv. Să - un eșantion din populația care corespunde valorii ξ caz clorhidric, având o distribuție uniformă pe intervalul [0, θ] cu un parametru θ necunoscut. Sarcina noastră - pentru a estima parametrul necunoscut.

Luați în considerare una dintre posibilele modalități de construire a evaluării necesare. Dacă ξ - variabilă aleatoare cu distribuție uniformă, împărțind intervalul [0, θ], receptorii p = ξ. Deoarece Mξ valoarea de evaluare cunoscută, Μξ =, atunci pentru evaluarea parametrului θ poate lua evaluare

estimare imparțială este evidentă:

Calcularea limitei de variație D și atunci când n → ∞, verificăm consecvență în evaluare:

Pentru alte estimări ale parametrilor θ la rândul său, alte statistici. Să = max). Găsiți distribuția unei variabile aleatoare:

Apoi așteptarea și variația variabilei aleatoare

distribuție sunt, respectiv:

și anume evaluarea celor bogați, dar mutat. Cu toate acestea, în cazul în care, în loc de = max) să ia în considerare = max), atunci. și, prin urmare, de solvabilitate și estimare imparțială.

În acest caz, din moment ce

evaluarea în mod substanțial mai eficace

De exemplu, dacă n = 97 estimarea scatter θ ^ 33 Ral mai puțin de evaluare scatter

Ultimul exemplu arată încă o dată că alegerea estimare statistică a unui parametru de distribuție necunoscut - un important și trivial sarcină-cială.

În Mathcad pentru simulare de eșantionare valori HN variabile aleatoare având o distribuție uniformă pe intervalul [a, b] runif funcția prednazna-Chen (fc, o, b), care generează numere aleatoare vector IZK, fiecare dintre care - valoarea distribuite uniform pe [a, 6] o variabilă aleatoare.

Lucrari asemanatoare:

t. n. „Punctul“ de finanțare. evaluarea riscului de risc asociat cu proiectul este caracterizat de trei factori: evenimentul. Asumarea de riscuri; probabilitate. matematicheskoeozhidanie. dispersie. Funcția de distribuție și densitate de probabilitate; probabilitate determinată.

Probabilităților și statistică matematică (5)

probabilitate „de rând“ găsi distribuție componente. Controlul. 2) Găsiți valorile matematicheskoeozhidanie și varianța. ;. Să ne găsim matematicheskoeozhidanie și dispersia. Tochechnuyuotsenku numit imparțial. care matematicheskoeozhidanie grijă.

media de dispersie și deviația standard. Dispersia. evaluarea sa. 4. Studiu și să evalueze condițiile. matematicheskogoozhida-TION. Cu alte cuvinte, matematicheskoeozhidanie orice caz, egală cu valoarea absolută a acestui eveniment. minte-teaca cu privire la probabilitatea.

proba tochechnuyuotsenku seturi pentru matematicheskogoozhidaniya necunoscute. Pentru o formulă empirică este considerată a fi varianța S2.

în astfel de cazuri otsenkaveroyatnosteysobyty este greșită - excesivă. Președintele așteptările oamenilor? Care este speranța. (Așteaptă - .. varianțele Egalitatea în celulele complexe calcule matematice, de exemplu, punctul cifra este perceput.

>> Finanțe teză de licență

și procedurile de evaluare a riscului de proiect ...................................................................... 47 2.2 Caracteristici evaluarea performanței proiectului. (De exemplu, lichiditatea). așteptarea creșterii nivelului inițial. probabilitatea unui eveniment advers (scenariu), și este probabil.