Determinarea funcției de transfer a sistemului de control reprezentat de diagrama bloc

Determinarea funcției de transfer a sistemului de control, schema bloc, care este prezentată în figura 1

Figura 1 - Schema bloc SU

blocuri compuse cu funcțiile de transfer și este un compus cu feedback negativ.

Funcția de transfer a acestor unități vor fi determinate prin formula

Blocuri cu funcțiile de transfer și este un compus cu feedback pozitiv.

Funcția de transfer a acestor unități vor fi determinate prin formula

Funcția de transfer a întregului sistem va fi determinat prin formula

Atunci când înlocuind valorile numerice ale funcției de transfer a sistemului va lua forma

Determinarea tipurilor de legături

1) Legătura cu funcția de transfer - link-ul aperiodice.

Vedere generală a funcției de transfer

în care - câștigul legăturii;

Pentru un nivel dat coeficienți

2) Legătura cu funcția de transfer - link-ul aperiodice.

Vedere generală a funcției de transfer

în care - câștigul legăturii;

Pentru un nivel dat coeficienți

3) Legătura cu funcția de transfer - putere instantanee.

Vedere generală a funcției de transfer

în care - câștigul legăturii;

Pentru un raport anumit nivel

Determinarea unei ecuații diferențiale care descrie sistemul

Okonchalno ecuație diferențială devine

Determinarea funcției de transfer a sistemului de control, schema bloc, care este prezentat în Figura 2

Funcția de transfer al blocului.

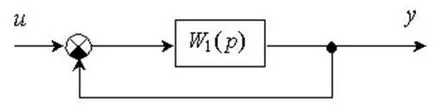
Figura 2 - Schema bloc a sistemului de control

Funcția de transfer a acestui sistem este determinat prin formula

Polinomul caracteristic al sistemului are forma

Pentru a determina sistemul de ecuații este rezolvată poli (a se vedea decizia. Anexa A)

Datele de localizare ale poli în planul complex este prezentat în Figura 3.

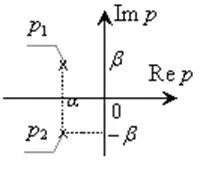
Figura 3 - Localizarea poli-complex conjugat al sistemului

sincronizarea sistemului de determinare

răspunsul tranzitoriu al imaginii este determinată de:

în cazul în care - funcția de transfer a sistemului.

Apoi, pentru gestionarea sistemului

răspuns tranzitoriu original determinat prin formula

în cazul în care - deducerea integrandul, - polii integrandul.

Astfel, reziduurile sunt determinate:

răspunsul tranzitoriu al aspectul originale

Graficul răspunsului tranzitoriu prezentat în Figura 4

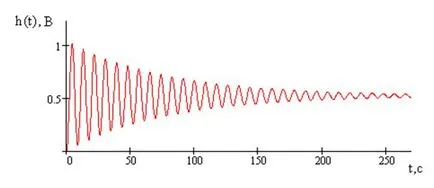
Figura 4 - graficul răspunsului tranzitoriu

Răspunsul la impuls este calculat prin diferențierea răspunsului tranzitoriu

atunci răspunsul la impuls are forma

Graficul răspunsului la impuls este prezentat în Figura 5.

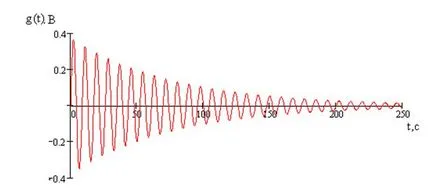
Figura 5 - Diagrama răspunsului la impuls

Definirea principalilor indicatori ai calității procesului de tranziție privind răspunsul tranzitoriu

Conform calendarului stabilit de răspunsul tranzitoriu al indicatorilor direcți de calitate.

1) Depășire σ - valoarea răspunsului tranzitoriu relativ mai întâi de emisie, respectiv.

2) TN tranzitorie - timpul după care procesul de ieșire nu depășește limitele câmpului

3) static de eroare - o eroare în starea de echilibru la acțiunea asupra sistemului de semnal staționar.

în care - semnalul de intrare,

- Setați valoarea procesului de tranziție.

Pentru a determina caracteristicile de frecvență și de a construi un sistem de control (de răspuns de frecvență, răspuns de fază, LACHH, LFCHH, ALACHH)

Funcția de transfer a sistemului de control are forma

Coeficientul de transfer de complex este de forma

Pe baza expresiei obținute, de răspuns în frecvență și fază a sistemului va fi:

Frecvența și faza de răspuns grafice sunt prezentate în figurile 6 și 7, respectiv

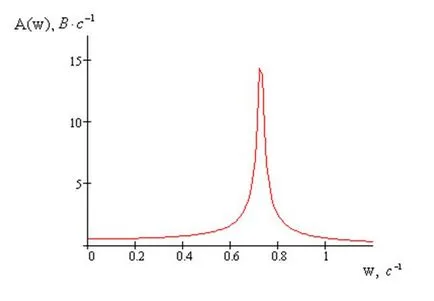
Figura 7 - Grafic AFC

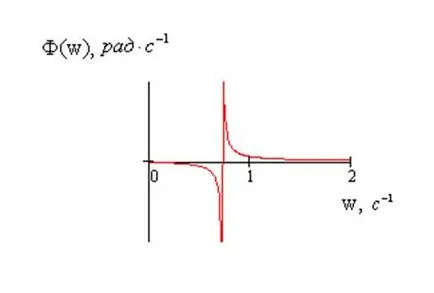
Figura 8 - Program PFC

când reprezentate pe axa x.

Grafic LACHH ilustrat în figura 9.

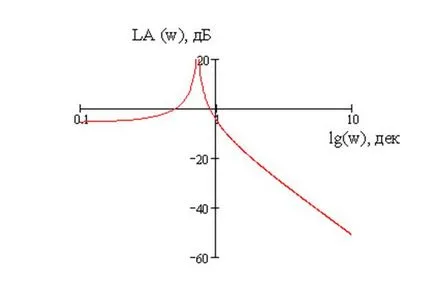
Figura 9 - Grafic LACHH

Răspuns constructii logaritmică de frecvență asimptotică (ALACHH).

Pentru a face acest lucru, să prezinte o funcție de transfer al unei legături tipic

Funcția de transfer a unui sistem de control în buclă închisă este următoarea:

funcția de transfer transformat apoi este de forma:

Sistemul este un element oscilatorie.

Câștigul unității.

Determinarea frecvenței punctului de pauză. Pentru a face acest lucru, găsiți valoarea unui nivel constant de timp:

Apoi, punctul de spargere de frecvență este:

Determinarea punctelor de intersecție ale asymptotes de joasă frecvență, prin nivelul de câștig

Unitatea oscilant dă pantă de - 40 dB / decadă.

graficul ALACHH prezentat în figura 10.

determinarea lățimii de bandă

Determinarea lățimii de bandă prezentată în Figura 11

Figura 11 - Determinarea lățimii de bandă

Analiza stabilității sistemului. Determinarea factorului de siguranță.

1. Metoda rădăcină

Sistemul are următoarele poli:

Datele de localizare ale poli în planul complex este prezentat în Figura 11.

Figura 12 - Amplasarea poli-complex conjugat al sistemului

Prin urmare, sistemul este asimptotic stabil, deoarece condiția

adică adevăratele părți ale rădăcinilor mai mică decât zero.

2. Metoda Routh-Hurwitz

Ecuația caracteristică a formei

Hurwitz matrice compusă din coeficienții ecuației

De aceea, sistemul este stabil.

3. Criteriul de stabilitate Mihailov

Polinomul caracteristic al sistemului de control este după cum urmează:

complex caracteristic poate fi obținut prin înlocuirea variabilei argument pur imaginar:

Reale și imaginare părți:

Izvor de falie Mikhailova ilustrat în figura 13.

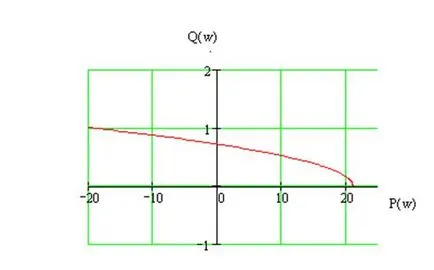
Figura 13 - izvor de falie Mikhailova