Definiți programul toate valorile momentului forței de frecare și de a găsi valoarea medie
2. Se determină programul toate valorile momentului forței de frecare și găsi mediu. Comparați acest rezultat cu cel măsurat anterior în muncă.
Target 3. Compararea valorilor măsurate și calculate ale momentelor de inerție
1. Se scrie în tabelul 2.4 rapoartele valorilor măsurate ale momentelor de inerție al pendulului.
2. Folosind formula pentru a calcula momentele de inerție organismelor geometrically regulate și teorema lui Huygens - Steiner calcularea momentelor de inerție ale scripeților, cruci și mărfuri, prin rotație în jurul unei axe care nu trece prin mijloc lor. Datele de calcul sunt luate din „pașaportul“ al dispozitivului. Momentul de inerție totală a pendulului se obține prin însumarea momentelor de inerție ale pieselor pendul.
3. Comparați valorile calculate și măsurate ale momentelor de inerție. Găsiți abaterile relative între calculate și momentele de inerție măsurate.
DEFINIREA MOMENTUL INERȚIA ȘI VERIFICAREA teoremei Huygens-Steiner
PRIN torsionale VIBRATII
Scopul de verificare experimentala a teoremei lui Huygens - Steiner și momente definitorii de inerție ale corpurilor de formă simplă. Ideea experimentului
Experimentul folosește legătura dintre perioada de oscilație a unui pendul de torsiune și momentul său de inerție. Ca pendul selectat platforma circulară, suspendată într-un câmp gravitațional pe trei filamente lungi (suspensii trifilyarny). Platforma poate efectua oscilații de torsiune în jurul axei verticale. Pe corp platforma de diferite forme plasate, măsurate perioadele de oscilație a unui pendul și valori ale momentelor de inerție ale organismelor stabilite. Teorema Huygens - Steiner verificată pentru consecvență între dependentelor experimentale și teoretice momentele de sarcini de inerție de pe distanța lor față de centrul platformei.

unde w - viteza unghiulară de rotație, J - momentul de inerție în raport cu axa de rotație M - momentul forțelor externe în raport cu această axă.
Teorema lui Huygens - Steiner. În cazul în care momentul de inerție în raport cu o axă de rotație care trece prin centrul de masă are o valoare de J0. că în ceea ce privește oricare altă axă la o distanță de la primul și paralel la acesta, va fi egală cu
unde m - masa corpului.
Pentru a verifica teorema lui Huygens - Steiner a studiat în această lucrare vibrațiilor de torsiune într-o suspensie de corp trifilyarnom solid. Trifilyarny platforma de suspensie este o rază circulară R, suspendat pe trei filamente dispuse simetric lungime egală armat, la marginile acestora (vezi fig. 8). Deasupra acestor fire sunt de asemenea simetric atașate la discul de dimensiuni ceva mai mici (raza r). Platforma poate efectua oscilații de torsiune aproximativ o ¢ axa OO vertical, perpendicular pe planul său și care trece prin centrul său. O astfel de mișcare platformă conduce la o schimbare în poziția centrului său de înălțimea gravitației.
Dacă platforma de masă m, se rotește într-o direcție, a crescut la o înălțime h, apoi
incrementul potențialului energetic este egală cu
unde g - accelerația gravitațională. Rotirea în cealaltă direcție, platforma vine la echilibru poziție (h = 0), cu o energie cinetică egală cu
unde J - momentul de inerție al platformei, W0 - viteza unghiulară de rotație a platformei de la momentul în care trece în poziția de echilibru.
Neglijând activitatea forțelor de frecare pe baza legii de conservare a energiei mecanice, avem:
Presupunând că platforma efectuează vibrațiilor de torsiune armonice pot fi scrise de dependența de timp a deplasării unghiulare a unei platforme sub formă de t
unde a - deplasarea unghiulară a platformei, a0 - unghiul maxim de rotație a platformei, adică amplitudinea deplasării unghiulare, T - perioada de oscilație. Pentru w vitezei unghiulare, care este derivata prima dată amploarea deplasării poate fi scris
În momentele de trecere a platformei prin poziția de echilibru (t = 0, 0.5T, ...), cantitatea w (t) este maximă și este egală cu
Din expresiile (3.5) și (3.8) rezultă că
Dacă lungimea I a filamentului de suspensie, R - distanța de la centrul platformei pentru firele punctelor de fixare pe ea, r - raza discului superior (. Figura 8), este ușor de văzut că
și cu o abatere maximă a platformei de la poziția de echilibru
La unghiuri mici de deflexie a0 sinusul unghiului poate fi înlocuit cu o valoare a0. Având în vedere, de asemenea, că atunci când R< Legea conservării energiei (2.9) ia forma: ceea ce implică faptul că Conform formulei (3.16) poate fi experimental determina momentul de inerție al corpului platformei sau platforma gol pus pe ea, ca toate cantitățile de pe partea dreaptă a formulei este măsurat direct. Trebuie amintit că m - este masa totală a platformei de testare și corpul culcat pe ea. Tipul instalației este prezentată în Figura 8. Raportul dintre raza a lungimii suspensiei platformei firelor R / l <0,05, что соответствует приближениям, используемым при выводе формулы (3.16). Organele platformei trebuie să fie pus strict simetric, astfel încât nu este platforma înclinată. Pentru a facilita determinarea poziției bunurilor și mai precis pentru a le instala pe platforma de trasat linii radiale și cercuri concentrice la o anumită distanță unul față de celălalt (5 mm). puls rotațională necesare pentru a declanșa oscilațiilor torsionale, potrivit unei platforme de disc rotativ, în jurul axei sale. Acest lucru se realizează cu ajutorul unui levier montat pe discul superior. Atunci când o astfel de excitație aproape nici o altă oscilație a căror prezență complică măsurătoarea. În măsurătorile, utilizarea amplitudinile de vibrații inacceptabile mai mari de 10 °. Măsurarea oscilațiilor poate fi realizată manual sau prin utilizarea unui cronometru sau cronometru. Ținta 1. Măsurarea momentului de inerție al platformei gol Măsurarea și prelucrarea rezultatelor 1. Momentul de inerție al platformei gol JPL definită de (3.16). Astfel, perioada de platforma T oscilație golească eroarea determinată experimental, iar valorile l, R, r, m și erorile lor sunt instalate permanent. 2. relatărilor, platforma de impuls rotativ și numărul tnekotorogo timp (N = 15 -20) oscilațiilor complet. O astfel de măsurătoare a fost repetată de 3 - 5 ori. Rezultatele obținute sunt înscrise în tabelul 3.1 al raportului. 3. Conform datelor experimentale pentru fiecare experiment sunt valoarea perioadei de oscilație torsional. 4. Găsiți valoarea medie și eroarea totală a perioadei de oscilație. În această eroare sistematică în perioada de măsurare, poate fi luată egală. 5. Se calculează momentul de inerție platformei JplE. Găsiți valoarea erorii relative și absolute pentru momentul de inerție al platformei. 6. Se calculează momentul teoretic al platformei inerție JplT. în funcție de greutatea și dimensiunea sa. Găsiți erori din acest calcul. 7. Comparați măsurate experimental și valoarea momentului de inerție al platformei gol calculată teoretic. Indicați ce procent din experimentale Valoarea diferă de :. teoretic Sarcina 2. Determinarea momentelor de inerție corpurilor o formă predeterminată Măsurarea și prelucrarea rezultatelor 1. Platforma încărcate alternativ organisme cercetate, astfel încât centrul de greutate coincide cu axa de rotație a platformei. Deoarece corpurile de placă de testare sunt selectate având forma unui pătrat, un dreptunghi, un triunghi echilateral, disc, precum și alte forme de corp geometric regulat. 2. Se măsoară numărul de oscilații pe parcursul întregului sistem. Pentru fiecare corp de măsurare se efectuează de 3 - 5 ori. Rezultatele măsurătorilor sunt introduse în tabelul 3.2 al raportului. 3. Se calculează momentele de inerție JN platformelor încărcate și erorile lor. Trebuie remarcat faptul că în ecuația (3.16) trebuie înlocuită cu cantitatea de masă a corpului și a platformei ca în eroare de eroare de eroare formula greutate egală cu greutatea totală a corpului și a platformei. 4. Folosind faptul că momentul de inerție - aditiv cantitatea se calculează momentele de inerție corpuri: JE = JN - JplE. Găsiți valoarea absolută și eroarea relativă pentru momentele de inerție corpurilor. 5. O comparație a valorilor obținute experimental ale momentelor de inerție cu calculat teoretic (a se vedea paragraful. Anexa 3). Rezultatele de calcul sunt înscrise în tabelul 3.3 al raportului. Sarcina 3. Verificați teorema lui Huygens - Steiner Teorema 1. Pentru a verifica Huygens - Steiner folosesc două sau mai multe organisme similare, având o formă cilindrică. 2. Instalați sarcini în centrul platformei, punându-le una peste alta. Excite platforma de vibrații de torsiune. Se măsoară timpul t câteva oscilații (N = 15 - 20 de). Datele sunt introduse în tabelul 3.4 al raportului. 3. Include o sarcini simetrice pe platformă în raport cu axa de rotație. Carry timp de măsurare a vibrațiilor pentru 5 - 7 poziții de mărfuri, le deplasează treptat la marginile platformei. 3.4 Valorile tabelate ale distanțelor de la centrul de masă al fiecărui corp și centrul platformei, precum și numărul de oscilații N timp tN acestor vibrații. Prelucrarea rezultatelor 1. 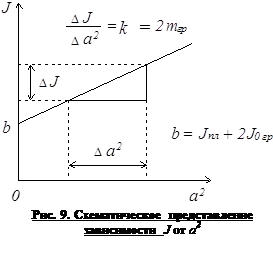
2. Valorile tabelate ale 2.
3. Pentru fiecare poziție sunt marfă momentul de inerție Ji cu încărcăturile platforma de la formula (3.16).
4. Valorile obținute ale momentului de inerție Ji este aplicată graficul momentului de inerție al organelor de sistem ale distanței pătrat la centrul de masă al mărfurilor și axa de rotație 2 (schematic această relație este prezentată în Fig. 9). Astfel cum rezultă din teorema lui Huygens - Steiner, acest grafic ar trebui să fie o linie dreaptă cu coeficient unghiular
cient de 2mgr numeric egal. în cazul în care mgr - masa încărcăturii. De asemenea, intercepta pe axa ordonată este suma momentelor de inerție a încărcăturilor platforma neîncărcate și momentele de inerție JPL + b = 2J0gr.
5. Din dependența J = f (a 2) determinarea valorii și valoarea mgr b. Comparând valoarea obținută cu sarcina de a fi utilizate în lucrare, iar valoarea obținută b cu valoarea calculată. Coincidența acestor valori (pentru calcule de erori) confirmă, de asemenea, teorema lui Huygens-Steiner.
DEFINIREA MOMENTUL Inerția forțelor roată de manevră de frecare în lagărele Obiectiv
ROȚI și forțele de frecare în lagărele MOMENT
Determinarea momentului de inerție al roții și momentul forței de frecare în lagăr, folosind legea conservării și transformării energiei. Ideea experimentului
Experimentul folosește o roată masivă, montat pe un arbore orizontal. Roata este condus de o rana cablu de pe arbore, care este atașat la sfârșitul sarcinii.
Momentul de inerție - o măsură de inerție a corpului în mișcare de rotație. Trebuie amintit că, în general, momentul de inerție poate avea valori diferite în ceea ce privește diferite axe de rotație a corpului. În cazul în care corpul are o formă arbitrară și o distribuție arbitrară a masei, momentul de inerție poate fi determinată prin însumarea aproximativă
,
unde ri - distanța de la axa de rotație la i-masa elementară Dmi.
În cazul în care corpul are o formă geometrică regulată și o densitate constantă în întregul volum, suma poate fi înlocuită prin integrarea pe întregul volum

Pentru a calcula momentele de inerție corpurilor având o formă geometrică simplă (disc, tijă, pătrat, etc.) sunt de obicei preparate prin (apendicele 3).
În cazurile în care calculul momentelor de inerție ale corpului este dificil, utilizați o varietate de moduri de a le măsura. Mai multe astfel de metode discutate în acest atelier. În această lucrare ne propunem abordarea de energie pentru a determina momentul de inerție.
Volantul (Fig. 10) constă dintr-un volant A montat fix pe un ax orizontal, arborele B. în cordonul este înfășurat, al cărui capăt este atașat la o greutate de m, care sub forța arborelui greutate poate fi nerăsucite. La rotirea unui corp cu momente de forțe care împiedică rotația acestuia. Aceste puncte sunt în principal forțele de frecare în suporturile și, în parte, forța de rezistență a aerului. Ultima în această lucrare nu este considerată din cauza micimii sale. Amploarea momentului forțelor Mtr frecare în lagărele pot fi stabilite, de exemplu, starea de echilibru M - Mtr = 0, precum și pierderea de energie a unui corp de rotație, așa cum se face în această lucrare. O picătură de potențial energetic MGH1 H1 de marfă este de a crește energia cinetică a translației
deplasarea mv marfă 2/2, pentru a crește energia cinetică Jw 2/2 o mișcare de rotație a volantului și arborele de instrumente și funcționare notare Mtr = A j pentru a depăși frecarea în lagăre. Conform legii conservării energiei
unde j1 - deplasarea unghiulară a arborelui în lagăr, corespunzător al încărcăturii de deplasare h1.
Alimentați mișcare uniform accelerată, fără viteză inițială, așa
unde t - coborârea unei H1 înălțime de timp. Viteza unghiulară a volantului
unde r - raza arborelui B. Moment Mtr forța de frecare este setat după cum urmează. Roata se rotește prin inerție, ridicarea sarcinilor la înălțime h2 Exprimându calea unghiulară (j1 + j2) prin linia (h1 + h2) și raza r a arborelui, obținem Această expresie este formula de lucru pentru măsurarea Mtr. Substituind în (4.1) valorile v, w, Mtr (4.2), (4.3), (4.6), obținem formula de operare pentru determinarea momentului de inerție al volantului În pregătirea pentru măsurarea cordonului volantului este înfășurat pe un turn ax pentru a porni. Până la sfârșitul platformei din cordonul ombilical atașat de greutate cunoscută, care sunt aplicate sarcini din setul care urmează să fie instalat. Pentru a măsura înălțimea h1 picătură de transport maritim și h2 de a ridica înălțimea instalării sale lângă bar la scară fortificata. Picătură de transport maritim de timp este măsurat cu un cronometru electronic sau fix de mână. inerție de măsurare a cuplului 1. Ținta moment al volantului și forța de frecare 1. Suport se măsoară raza arborelui. 2. Înălțimea de cădere de transport maritim H1 în toate testele puteți lua la fel. Prin urmare, poate fi pre-măsurată ca distanța dintre preselectat superioară Poziția Georgiei și poziția sa atunci când cordonul complet deșirat. 3. Cablu de cilindru cu arborele, ridicarea sarcinii până la punctul selectat. Platforma pune o greutate dintr-un set. Se măsoară timpul de scădere la sarcină maximă detensionarea cablului. 4. Se măsoară înălțimea h2. care se ridică de sarcină, după detensionarea cablului. 5. Experiența cu o marfă repetată de cel puțin trei ori. Apoi, măsurarea se face cu două și trei sarcini. Toate datele sunt introduse în tabelul 4.1 al raportului. 1. Din formulele (4.6) și (4.7) pentru fiecare punct de masă se calculează forța de frecare în lagărele și momentul volant de inerție, prin substituirea valorilor medii ale t și înălțimea h2 timpului. 2. Găsiți o valoare medie a momentului de inerție al volantului. Nu are nici un sens pentru a găsi valoarea medie a momentului forțelor de frecare, deoarece sarcini diferite pe arborele trebuie să aibă valori diferite. 3. Erori de măsurare a momentului de inerție se propune să evalueze experiența uneia dintre sarcinile. Valoarea obținută a erorii relative a momentului de inerție poate fi aplicat la valoarea medie a momentului de inerție. Trebuie luate Valorile erorilor de măsurare sistematice de înălțimi H1 și H2, în funcție de condițiile concrete de măsurare. Erori de încărcături platformă de măsurare mase egale și ± 0,5 g. Informații despre „Cinematica și dinamica mișcare înainte“ Categorie: Fizică
Numărul de caractere, inclusiv spații: 136 506
Număr de mese: 5
Număr poze: 32