Conceptul de deconvoluție

Pentru reprezentarea fizică suficient de complexă în timpul (coordonate) al regiunii ușor de înțeles deconvolution în reprezentarea de frecvență. Să presupunem că un sistem de înregistrare are loc de absorbție a energiei de rezonanță și schimbare de fază a vibrațiilor armonice de la un semnal de intrare constând din, de exemplu, armonică păcat conversie w0 t ® 0.5 sin (w0 -p / 4). Prin urmare, pentru a restabili funcționarea inițială de undă deconvoluție este de a realiza această amplificare armonici în semnalul de ieșire de 2 ori și să efectueze o schimbare de fază inversă de p / 4. Pentru o performanță armonică a unei astfel de operațiune nu este de lucru. Dar problema practică deconvoluție este mult mai dificilă, deoarece necesită, de regulă, recuperarea completă a spectrului semnalului original, având un caracter continuu.

Determinarea deconvoluție. Dacă convoluția directă semnal digital x (k) c impuls de răspuns h (n) a sistemului liniar (filtru) au ecuația:

y (k) = h (n) # 9314; x (k) ó H (z) X (z) = Y (z), Y (z) = yk z k. z = exp (-jj),

problema deconvolutie în formă generală - determinarea semnalului la intrarea sistemului liniar pentru valorile semnalelor de ieșire, adică reacția de îndepărtare (răspuns la impuls) sistemului asupra semnalului și restabilirea formei de undă originală, care este foarte important, de exemplu, pentru sistemele de înregistrare:

X (z) = Y (z) / H (z) = Y (z) H -1 (z) ó y (k) # 9314; h -1 (n) = x (k), (13.1.1)

unde subscriptului "-1", funcția de transfer simbolic desemnat filtru operatorul invers H -1 (z) = 1 / H (z), adică, Operatorul deconvoluție, operatorul sinuozitate directă inversă (sistem de răspuns la impuls). Prin urmare, atunci când operatorul revers deconvoluție-z transformarea obține:

H -1 (z) = 1 / H (z) ó h -1 (n). (13.1.2)

Evident că, în cazul în care există un H (z) H -1 (z) = 1, atunci invers z transforma această expresie, trebuie să avem:

H (z) H -1 (z) = 1 ó h (n) # 9314; h -1 (n) = do (n), (13.1.3)

unde do (n) - puls Kronecker. În acest convoluție secvențială a semnalului x (k) cu h operatorul de sistem (k) și operatorul de deconvoluție h -1 (k) este echivalentă cu convoluția a semnalului x (k) cu un puls Kronecker care nu trebuie să modifice semnalul de formă x (t).

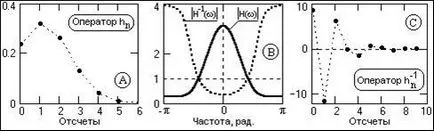
Când z = exp (-jj) Toate cele de mai sus se aplică și la reprezentarea spectrală a operatorilor. Un exemplu al operatorului de inversie printr-o reprezentare spectrală este prezentată în Fig. 13.1.1 (original operatorului hn ® densitate spectrală H (# 969;) ® inversă densitate spectrală H -1 (# 969;) ® inversă operatorului h -1 n în probele de interval inițial).

Caracteristici deconvoluție. Ecuația (13.1.2) vă permite să facă unele concluzii cu privire la particularitățile de efectuare deconvoluție.

nu Când finit h răspuns la impuls (n) operatorul invers h -1 (n) este în general limitată. De exemplu, în cazul în care răspunsul la impuls este reprezentat de un dipol h normalizat (n) = ó (1 + az) = h (z), atunci avem:

H -1 (z) = 1 / (1 + az) = 1-az + a2-a3 z 2 + z 3.

Este într-adevăr aproape orice operatori convoluție a căror energie pe zonele restricționate ale principalelor gama de frecvențe aproape de zero. Când funcția spectrală inversare a operatorilor din aceste zone cu vârfuri ascuțite spectrale care transformarea Fourier inversă este lăsată să se degradează încet operatorii de funcții. Un exemplu al acestui fenomen este prezentat în Fig. 13.1.2.

Rezultă că pentru a efectua cu exactitate deconvoluție este necesar să existe un operator de filtru invers infinit lung. În practică, deconvoluția se efectuează în cazul în care operatorul invers dispare rapid și poate fi limitată. Dar utilizarea operatorilor trunchiate dă naștere la o anumită deconvoluție eroare, valoarea care ar trebui să fie monitorizate.

Rețineți, de asemenea, că funcțiile de transfer ale sistemelor tind să aibă un caracter low-pass. Inversând operatorii acestor sisteme este întotdeauna asociată cu amplificarea frecvențelor înalte, ceea ce duce la inverse de mare câștig filtre variației zgomotului, ceea ce poate duce la pierderea semnalului dorit între fluctuațiile de zgomot amplificate.

În plus, dezintegrarea rapidă a operatorului deconvoluție este o condiție necesară, dar nu suficientă pentru punerea în aplicare a deconvoluția.

Stabilitatea filtrelor deconvoluție. Funcția H (z) în expresia (13.1.2) are puncte singulare - zerouri funcționale, stâlpi care devin funcția H -1 (z) = 1 / H (z) și determină stabilitatea filtrului invers. Pentru deconvolutie filtru să fie stabil, un număr de 1 / H (z) ar trebui să conveargă, adică polii funcției ar trebui să fie în afara cercului unitate pe planul z (în interiorul cercului folosind simboluri z -1).

H (z) polinom de ordinul N poate fi descompus în factori de prim N - binomi (dipolare):

unde a, b, c, ... - rădăcini ale unui polinom. Manipularea funcției de transfer:

Dacă fiecare dintre funcțiile dipolare (13.1.4) este un dirakoidom cu fază minimă, adică dipole rădăcinile sunt în afara cercului unitate în modulele z plane și membre ale dipol zero, sunt întotdeauna mai mult în urma în urma lor primii membri (în acest caz: | o |> 1 | b |> 1 | o |> 1), funcția H ( z) este de asemenea un dirakoidom cu fază minimă. Energia maximă a răspunsului la impuls dirakoida fază minimă este concentrată în partea sa inițială, și numără un număr de secvență este amortizată. Funcția 1 / H (z) va fi, de asemenea, o funcție de transfer de operator minim faze asigură condiția (13.1.3) și ei inversă - filtru seria convergent stabil. De exemplu, un filtru care implementează o funcție de transfer (13.1.5), în forma sa cea mai generală, se poate face sub formă de filtre conectate în serie, fiecare dintre care are o funcție de transfer de tipul următor (pentru primul filtru):

De aici, precum și direct din expresia (13.1.5), rezultă, de asemenea, că o mai mare valoarea modulelor de filtrare rădăcini (mai departe de cerc filtru pol unitate), cu atât mai rapid dezintegreaza operatorul invers.

Verificați stabilitatea operatorului filtrului invers în Mathcad este prezentată în Fig. 13.1.3. Module toate rădăcinile mai mari decât 1, polii polinomiale inverse sunt în afara cercului unitate pe planul z, operatorul invers și trebuie să fie stabil.

Cifra arată, de asemenea operatorul deconvoluție care se obține prin Fourier inversă transformare a funcției de transfer Hi (w). Operatorul este fără sfârșit, dar dispare rapid, ceea ce asigură o deconvoluție de mare precizie cu ajutorul unui număr limitat de membri ai operatorului de filtrare (setat de utilizator pentru o anumită precizie).

Fig. 13.1.3. EXEMPLU filtru invers stabil.

Exemplul 2: Să ne schimbe declarația de mai sus de către o poziție la dreapta și de a menține același operator de energie va avea H0 = 0,001. Este necesară pentru a evalua stabilitatea inverse operatorului convoluție HN =, N = 7.

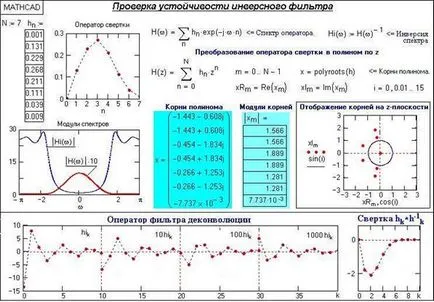
Fig. 13.1.4. EXEMPLU filtru invers instabil

Rezultatele testelor efectuate asupra noii rezistența operatorului deconvoluție prezentat în Fig. 13.1.4. Cu o formă similară a operatorilor convoluție module ale spectrului sunt practic identice. Dar, din cauza defazarea operatorului în raport cu primul (Fig. 13.1.3), rădăcinile sale z-polinomială a suferit modificări semnificative, iar modulul este una dintre rădăcinile mai mic decât 1. Deși operatorul deconvoluție calculat reprezintă de asemenea un număr de energie finit, dar condiția (13.1.3) nu este îndeplinită, așa cum este demonstrat de rezultat convoluție hk * h -1 k.

Manipularea funcțiilor nedirakoidnyh. Dacă H (z) - reversoid, adică rădăcini dipoli constituente situate în interiorul și pe cercul unitate din planul z, H circulație constantă (z) este antiimpulsom (cu puteri negative ale z) și de a folosi este necesar să aibă „viitor“ valoare a semnalului de intrare.

Dacă funcția dipolii (13.1.4) și reprezintă dirakoidy și reversoidy, tratamentul va fi determinat de centroidul totală și o serie Laurent:

și anume Operatorul de filtrare inversă este bilateral și nu neapărat simetrice, așa cum am discutat mai devreme, de obicei, operatorii bilaterale.

Exemplul 3. Filtru Funcția de transfer: H (z) = 1-2z. Funcția Inverse H -1 (z) = 1 / (1-2z). Spectrele de frecvență a funcțiilor prezentate în Fig. 13.1.5.

Polul zp = 1/2 funcție și stocată în interiorul cercului unitate pe planul z.

Rescriem expresia pentru inversul filtrului după cum urmează:

Această expresie este o extindere în puterile 1 / z și converge la cercul de rază 1/2 pentru z → ¥. Coeficienții puterilor 1 / z sunt, respectiv, coeficienții filtrului invers cu coordonate (N), adică filtru funcționează pe „viitor“ a eșantioanelor de semnal de intrare (vezi. Fig. 13.1.5).