Cat Arnold - grup Saratov dinamicii neliniare teoretice

Afișarea „pisica Arnold“

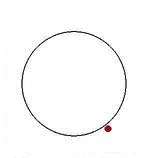
Este cunoscut în literatura de specialitate ca o reflectare a „Arnold pisica.“ (Prim valorile mărcilor ale variabilelor dinamice referitoare la următorul pas de timp discret.) Spațiul de fază a sistemului este de obicei interpretat ca suprafața unui torus, în care o variabilă este setat coordonata paralela, iar celălalt de-a lungul unui meridian al Torul, ambele fiind definite pe intervalul de la 0 la 1. pentru utilizare mai convenabil de ilustrații grafice unitatea pătrat, având în vedere că partea dispuse opus acesteia sunt identificate. Originea numelui se datorează faptului că domnul Arnold, care a propus această hartă ca un exemplu de sistem cu dinamica haotica pe pilier ilustrat acțiunea lui folosind imaginea în formă de cap de pisică (vezi. fig.).

Se afișează Arnold pisica aparține unei clase de sisteme conservatoare: sub influența orice zonă de afișare (de exemplu, capul pisicii) păstrează zona. Este cunoscut faptul că această hartă arată o dinamică haotică în sensul teoriei axiomatică a hiperbolică Anosov. Doi Lyapunov exponent pentru a afișa Arnold pisica

Rețineți că o figură centrală este pozitiv. Unele informații suplimentare despre afișarea Cat Arnold si alte harti pe pilier pot fi găsite în secțiunea de site-ul nostru dedicat haos cuantic.

Pentru mai multe util să rețineți că cartografiere Arnold pisica poate fi reprezentată ca o aplicație de două ori a unei simple de cartografiere

Revenind la punerea în aplicare fizică a ecranului pisica Arnold, ia în considerare cele patru oscilator cuplat van der neautonom Pol

Aici x. y. z și coordonate generalizate w oscilatoare, A - amplitudine ale parametrilor de modulare de control, T - perioada de modulație, care, după cum vom asuma conține numărul întreg de perioade de oscilații naturale 2 # 112; / # 119; 0. # 101; - parametru de cuplare.

Sistemul funcționează după cum urmează. Fie prima și a doua etapă de generare oscilator oscilează cu faze, respectiv Fx și ~ y.

în timp ce a doua pereche de oscilatoare este sub pragul lasing. În trecerea la o etapă de excitație a doua pereche, al treilea sistem oscilator z este expus semnal de semințe care corespunde xy produsului și care cuprinde un oscilator rezonant la această componentă de două ori frecvența:

Astfel, oscilațiile treia fază oscilator obținut Fz = Fx + ~ y. oscilator a patra w excitat doar la frecvența semnalului x # 119; 0 astfel încât Fw = Fx. Mai mult, atunci când generează etapa a doua pereche de capăt oscilatoare, w este semnalul de semințe pentru oscilatorul y. etapa de excitație de intrare și z semnal prin amestecarea cu un semnal de frecvență de referință # 119; 0. prevede oscilator de semințe x. dată de al doilea termen în formula

Ca rezultat, o nouă excitație pas faza prima și a doua oscilatoare obținute respectiv F'x = Fz = Fx + și F'y ~ y = Fw = Fx. Având în vedere că fazele sunt definite până la un aditiv 2 # 112; și introducerea variabilelor standardizate q = Fx / 2 # 112; și p = ~ y / 2 # 112;. Ajungem la p cartografiere „= q. q „= p + q (mod 1), utilizarea ai clorului care, așa cum sa menționat mai sus, echivalent cu cartografierea pisica lui Arnold. Următoarea figură arată relația dintre variabilele de timp x. y. z și w sunt deja in curs de o mișcare haotică, în conformitate cu mecanismul descris. Image pe baza rezultatelor din soluția numerică a ecuațiilor cu # 119; 0 = 2 # 112;. T = 20, A = 2, # 101; = 0,4.

Haosul se manifestă într-o plimbare aleator maximele și minimele plic în raport cu umplutura. Pentru a demonstra conformitatea cu dinamica fază a hărții pisica Arnold, pune în aplicare procedura de mai jos. Derulăm soluție numerică de ecuații, iar la un moment dat corespunzătoare etapei de mijloc de excitație a primului și al doilea oscilator determina fazele lor folosind relațiile

Dacă punctul cu coordonatele (Fx. ~ Y) se încadrează în „cap de pisică“, care o înfățișează în diagrama, iar în următoarele două grafice punct (Fx ~ y) prin timp 2T si 4T. După acumularea unui număr suficient de mare de puncte de război de țesut „cap de pisică“, iar imaginile sale după unul și două iterații de afișare Arnold. Imaginile rezultate pot fi comparate cu cele obținute direct de la iterații Arnold ale hărții. Conformitatea este îndeplinită dacă este introdusă în ambele ecuații constante de aditivi care îndeplinesc anumite adaos constant la faza apărută în predarea perturbațiilor între oscilatoare. Având în vedere acestea, selectate în mod empiric pentru un mod constant dat, afișajul este modificat, astfel:

Comparați cele două de mai jos o serie de diagrame pentru a asigura respectarea dinamicii remarcabile în fază a sistemului propus și dinamica hărții pisica Arnold modificat.

Ultima cifră este o reprezentare grafică a doi exponenți mai mari Lyapunov pentru sistemul cuplat de oscilatoare nonautonomous Van der Pol de modulare lent de amplitudine A la alți parametri fixe, și a primit pe unitatea de timp perioadă de 2T.

După cum se poate observa, o gamă largă de parametru ambele Lyapunov exponent rămâne aproximativ constant în bună concordanță cu valorile așteptate pentru afișarea Arnold pisica.

Notă. În cazul în care abordarea dinamica sistemului formal, în ceea ce privește construirea stroboscopică hărții Poincaré, se reduce la iterații ale unui ecran de 8-dimensional. Într-adevăr, starea instantanee a sistemului este determinată de un set de opt variabile V = x. dx / dt. y. dy / dt. z. dz / dt. w. dw / dt>. Dacă la un moment t instant = nT vector set de stat Vn. soluțiile ecuațiilor de stat explicit obținute prin perioada 2T. Vn + 1 = F (Vn). În difuzor spațiu 8-dimensional are loc în apropierea Torul bidimensionale, care pot determina coordonatele a două faze de cartografiere supunându pisica Arnold. Pentru restul coordonatelor este o compresie puternică.

grup Saratov
neliniar teoretic
difuzoare