Câmpul magnetic al unui solenoid infinit lung

Solenoid - o bobină de sârmă de formă cilindrică. Acesta poate fi reprezentat ca un set de bobine circulare suprapuse cu curent. Liniile de câmp magnetic generat de curentul electro-cal în solenoid sunt prezentate în Fig. 6.6. După cum se vede din această figură, aproape linii drepte de forță în interiorul solenoidului. Lungimile solenoid-l, adică lungimea mai mare în comparație cu raza sa, cea mai mică curbura liniilor de câmp în interiorul solenoidului. În acest caz, în vectorul de câmp magnetic de inducție în interiorul solenoidului este direcționat paralel cu axa sa. Și, astfel încât direcția sa se datorează direcția curentului în regula șurubului solenoid mână. Directăm axa x de-a lungul axei solenoidului. Proiecția vectorului inducție magnetică în axa x va fi egală cu valoarea absolută, iar toate celelalte proeminențele sale vor fi egale cu zero:

Substituind aceste proiecție vectorilor B în ecuația (6.12). obținem

Această ecuație implică faptul că în cadrul inducției magnetice solenoid nu numai își păstrează direcția sa, dar amploarea ei este peste tot la fel. Astfel, putem concluziona că lungimile în interiorul-picior ale câmpului magnetic al solenoidului este omogen.

Fig. 6.6. Câmpul magnetic al solenoidului

Găsim magnitudinea câmpului magnetic de inducție în interiorul electrovalva folosind Teorema (6.8) pentru circulația vectorului. Ca un con-rotund C, în care calculăm circulația inducției magnetice, selectați linia rupt, prezentată prin linii punctate în Fig. 6.6. Lungimea acestei lungimea liniei l este în interiorul solenoidului și coincide randamentele cu una dintre liniile de câmp magnetic. Două perpendicular pe acest segment de dreaptă încep de la capete și du-te la un infinit-Ness. La toate punctele acestor linii drepte sau vector inducție magnetică perpendicular pe acesta (în solenoid) sau zero (off solenoid). Prin urmare, produsul scalar Vdl la aceste puncte este egal cu zero. Astfel, circulația inducției magnetice a subiectului contur C este egal cu integralei liniei forței lungimea segmentului l. Având în vedere că modulul vectorului inducție magnetică este constantă va fi

Fie numărul de rotații ale solenoidului acoperit contur C este egal cu N. În acest caz, suma curenților de circuit acoperite va fi egal cu NI, în cazul în care I - curentul într-o singură bobină a solenoidului. Teorema (6,8) conduce la ecuația

din care vom găsi câmpul magnetic în solenoid:

n-numărul de rotații pe unitatea de lungime a solenoidului.

Câmpul magnetic al curentului

Luați în considerare un câmp magnetic produs de curent electric TEKU-conductoare pe fire subțiri infinit lungi. Un astfel de sistem are simetrie cilindrică. În consecință, câmpul magnetic trebuie să aibă următoarele proprietăți:

1) pe orice linie paralelă cu firul cu vectorul curent al inducției magnetice trebuie să fie peste tot odi-Nakov;

2) în întregime în jurul firului, nu se schimbă atunci când se rotește întregul câmp magnetic. În acest caz, liniile de câmp magnetic ar trebui să fie centrele de cerc care se află pe axa firului cu com (figura 6.7) și vectorul B în oricare dintre aceste cercuri pretutindeni are unul și același modul.

Folosind Teorema (6.8) pentru circulația modulului inducție TION magnetic va găsi acest vector. În acest scop, vom calcula circulația inducției magnetice a uneia dintre liniile de forță C, a cărui ra-și venele raza. Deoarece vectorul B este tangent la linia de forță, este coliniar cu un element de vector al liniei dl. prin urmare

unde B - unitate de inducție magnetică, care, așa cum sa spus, peste tot pe circumferința C este aceeași. Oferă semnul integrală. După integrarea va avea

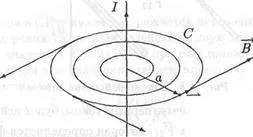
Fig. 6.7. Liniile de câmp magnetic ale curenților de direcți

Deoarece circuitul C include doar un singur fir care transportă un curent I, Teorema (6,8) conduce la ecuația

Prin urmare, constatăm că la o distanță de la un fir drept infinit transportă un curent I generat de câmpul magnetic ei vor

După cum se poate observa din Fig. 6.7, direcția vectorului B și direcția curentului I regula șurubului asociat dreapta. Faptul că acest lucru este adevărat, este ușor de a face cu ajutorul legii Biot - Savart - Laplace.

Luați în considerare două paralele subțiri unul cu celălalt fir direct cu I1 curenții și l2 (Fig. 6.8.). În cazul în care R distanța dintre conductoare este mult mai mică decât lungimea lor, câmpul de inducție magnetică generată de primul conductor în această distanță poate fi găsit de formula (6.15):

vector direcție B1 asociat cu direcția regulii I1 șurubul PRA-Vågå curent. Acest vector este prezentat în Fig. 6.8.

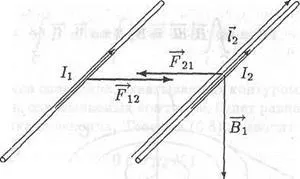
Fig. 6.8. interacțiune curentă

Câmpul magnetic produs de primul curent, va acționa pe sârmă Auto-Swarm cu Ampere forță F21, care este definit prin formula (5.8):

unde l2 - vector, a cărui lungime l este lungimea secțiunii considerată a doua sârmă. Acest vector este direcționat de-a lungul firelor de direcția curentului. Modul de alimentare (6.17) va

Substituind expresie (6.16) în (6.18), obținem următoarea expresie pentru forța care acționează asupra primei porțiuni conductoare a doua lungime a conductorului l:

Direcția forță F21 a găsit din formula (6.17). Când curentul I1. fluxul de l2 în aceeași direcție, această forță va fi îndreptată spre prima sârmă. Puterea F12. un al doilea fir care acționează pe porțiunea primei lungimii conductorului l, este egală în mărime și opusă în vigoare direcție F21.

Astfel, sa constatat că firele paralele cu curenții care curg în aceeași direcție se atrag. Este ușor să dovedească faptul că firele purtătoare de curenți în direcții opuse se resping reciproc.

Cu ajutorul formulei (6.19) este definit în unitatea curentă SI. După cum se știe, această unitate se numește Amperi. Prin definiție, două fire subțiri și lungi, cu forță de curenți într-un amper dispus la o distanță de 1 m de la un altul, de a interacționa cu putere 2 • 10 -7 N per 1 m lungime lel Paral. Înlocuind aceste valori în ecuația (6.19), constatăm că constanta magnetică

taxa de unitate SI - pandantiv - exprimat în termeni de o unitate de curent: Kd = A * p. Măsurarea forței de interacțiune a două sarcini punctiforme în 1 C a condus la o valoare F = 10 09 septembrie • H când distanța dintre tarifele R = 1 m. Folosind aceste valori, descoperim e0 electric constant de legea lui Coulomb

Este interesant de notat faptul că valoarea

numeric egală cu viteza luminii în vid.