Calcularea matricei metodei rang minori fringing

În subiectul anterior a fost considerat conceptul de rangul unei matrice, precum și exemplele care arată cum să găsească rangul prin definiție. Desigur, pentru a găsi rangul matricei, astfel, oarecum dificil - mai ales din cauza capacității de calcul. Cu toate acestea, suma calculată minori poate fi redusă substanțial prin utilizarea așa-numita metodă de fringing minori.

Metoda fringing minori au exprimat o pereche de puncte de un algoritm simplu:

Să o $ M $, pentru minor k nu este zero.
În cazul în care minorii fringing la minor $ M $ (este de a fi minori (k + 1)), comanda -lea pentru a face posibilă (adică matricea cuprinde rânduri sau coloane k k) egal cu rangul k. În cazul în care există minori și sunt toate înspre larg egal cu zero, atunci gradul egal cu k. Dacă printre minori învecinate să aibă cel puțin un non-zero, atunci repetați pasul №1, luând k + 1 în loc de k pentru ea.

În mod clar toate cele de mai sus poate fi exprimată prin următoarea schemă:

Calcularea matricei metodei rang minori fringing

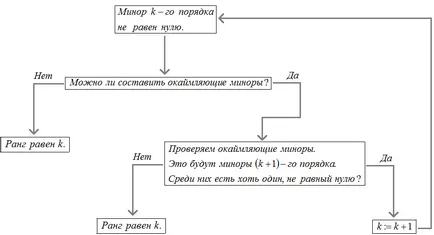
Voi explica acest circuit mai detaliat. Să vorbim încă de la început, adică, minorii cu prima comanda. Dacă toate primul ordin al unor minori matrice $ A $ (minori primul ordin - elementele matricei) sunt zero, atunci $ \ sunat A = 0 $. În cazul în care matricea este minor de ordin $ M_1 \ neq 0 $, atunci $ \ sunat A≥ 1 $.

Verificați minorii mărginesc pentru minore M_1 $ $. Acest lucru va fi deja minorii de ordinul al doilea. În cazul în care toți minorii, mărginesc M_1 $ $, egal cu zero, atunci $ \ sunat A = 1 $. În cazul în care în rândul minorilor de ordinul al doilea, mărginesc M_1 $ $, există cel puțin un minor $ M_2 \ neq 0 $, atunci $ \ sunat A≥ $ sau 2.

Verificați minorii mărginesc pentru minore M_2 $ $. Acest lucru va fi minorii de ordinul trei. Dacă toți minorii din al treilea ordin, se invecineaza cu M_2 $ $, egal cu zero, atunci $ \ A sunat = 2 $. Dacă printre minori de ordinul trei mărginesc M_2 $ $, există cel puțin un minor $ M_3 \ neq 0 $, atunci $ \ sunat A≥ 3 $.

Verificați minorii mărginesc pentru minore M_3 $ $. În cazul în care toți minorii unui al patrulea ordinul fringing M_3 $ $, egal cu zero, atunci $ \ sunat A = 3 $. Dacă în rândul minorilor a patra de ordinul mărginesc M_3 $ $, există cel puțin un minor $ M_4 \ neq 0 $, atunci $ \ sunat A≥ $, 4.

toate Verificăm invecineaza cu minori pentru minori $ M_4 $, și așa mai departe. În cele din urmă, există două posibilități: fie la un moment dat se dovedește că toți minorii sunt limitrofe zero sau pur și simplu fringing minore creează nu va funcționa, la fel ca în matricea „a alerga afară“, rânduri sau coloane. Ordinea ultimului minor de zero compilat și va fi egală cu rangul matricei.

Găsiți Locul de $ matrice A = \ stânga (\ începe -1 2 1 3 \\ -3 0 5 4 \\ -5 4 7 10 \ end \ dreapta) $ fringing de minori.

Puteți, desigur, să înceapă cu minorii de prim ordin, care sunt doar elemente ale matricei. Dar este mai bine să alegeți un non-zero, minoră de ordinul al doilea, cu atât mai mult că o astfel de alegere nu este de o mare complexitate. De exemplu, la intersecția liniilor №1, și coloane №1 nr.2, №2 sunt elemente minore \ $ din stânga | \ începe -1 2 \\ -3 0 \ end \ dreapta | $, care este simplu de a calcula, folosind formula №1 a firelor cu privire la calculul determinanților al doilea și al treilea ordin:

$$ \ left | \ începe -1 2 \\ -3 0 \ end \ dreapta | = -1 \ cdot 0-2 \ cdot (-3) = 6. $$

Deci, există minore de ordinul doi, nenulă, ceea ce implică faptul că $ \ sunat A≥ $ sau 2. Luați în considerare minorulii de ordinul al treilea care flanchează ordinea activă a doua minoră. Scrie fringing Minor? În acest scop, un set de rânduri și coloane la intersecția elementelor minore, care sunt de ordinul doi, trebuie să adăugați un alt rând și o altă coloană. Amintindu că elementele de contact sunt înregistrate de-al doilea ordin minor se află la intersecția rândurilor №1, №2 și coloane №1, №2. Adăugați mai multe rânduri la linia №3, iar coloanele - o coloană №3. Primim ordin al treilea minor ale cărui elemente (acestea sunt prezentate în figură în albastru) se află la intersecția liniilor №1, №2, №3 și coloane №1, №2, №3.

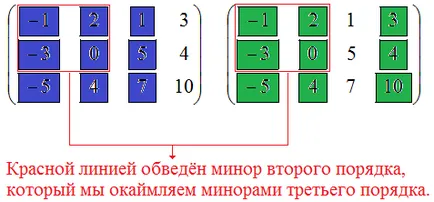
$$ \ left | \ începe -1 2 1 \\ -3 0 5 \\ -5 4 7 \ end \ dreapta | = 0. $$

zero, fringing Minor. Ce înseamnă acest lucru? Acest lucru sugerează că trebuie să continue identificarea minorilor dantelate. Fie că sunt toți zero (atunci gradul este egal cu 2), oricare dintre ele există cel puțin un non-zero.

Elemente de-a doua se invecineaza minciuna minoră la intersecția liniilor de №1, №2, №3 și coloane №1, №2, №4. Figura de mai sus prezintă elemente minore de culoare verde. Calculăm minorul, toate folosind aceeași formulă №2 a firelor cu privire la calculul determinanților al doilea și al treilea ordin:

$$ \ left | \ începe -1 2 3 \\ -3 0 4 \\ -5 4 10 \ end \ dreapta | = 0. $$

Și această fringing minoră este zero. Alte minori mărginesc acolo. În consecință, toate mărginesc minorii sunt zero. Ordinea ultimului minor nenulă este compus 2. Concluzie: Rangul este de 2, și anume, $ \ A = 2 Rang $.

Găsiți rangul de matrice $ A = \ stânga (\ începe 1 2 0 4 5 \\ 3 6 -2 -1 -3 -2 \\ -4 2 5 7 \\ -1 -2 2 9 11 \ end \ dreapta) $ fringing de minori.

Din nou, ca în exemplul precedent, începem cu decizia de selecție a doua ordine minore nu sunt egale cu zero. De exemplu, la intersecția liniilor №1, și coloane №1 nr.2, №2 sunt elemente minore \ $ din stânga | \ începe 1 2 \\ 3 6 \ end \ dreapta | $, care este simplu de a calcula, folosind formula №1 a firelor cu privire la calculul determinanților al doilea și al treilea ordin:

$$ \ din stânga | \ începe 1 2 \\ 3 6 \ end \ dreapta | = 1 \ cdot 6-2 \ cdot 3 = 0. $$

Minor activ de ordinul zero, adică alegerea nu are succes. Ia-o ordine minoră a doua. De exemplu, elementele care sunt situate la intersecția rândurilor №1, și coloane №2 nr.2, №3:

Astfel, nenulă minoră a doua ordine acolo, deci $ \ sunat A≥ $ sau 2. Notam ca un minor $ M_2 $ și devin tăiate minori sale de ordin al treilea. De exemplu, pentru a adăuga rânduri și coloane, pe care există elemente ale $ M_2 $, mai mult linia №3 și coloana №1. Ie găsi ordin al treilea minor ale cărui elemente sunt la intersecția rândurilor №1, №2, №3 și coloane №1, №2, №3. Noi folosim formula №2 a firelor cu privire la calcularea factorilor determinanți ai doua și a treia comenzi. Calculele detaliate I conduc nu, scrie doar răspunsul:

$$ \ din stânga | \ începe 1 2 0 \\ 3 6 \\ -2 -2 -4 2 \ end \ dreapta | = 0. $$

Acest lucru minor este zero, atunci ai nevoie pentru a trece la un alt minor fringing. Fie toți minorii din al treilea ordin, mărginesc M_2 $ $, egal cu zero, oricare dintre ele încă mai există cel puțin un non-zero.

Luați în considerare elementele minore de ordinul al treilea se află la intersecția liniilor №1, №2, №3 și coloane №2, №3, №4. Acest minor este, de asemenea, marginita M_2 $ $:

$$ \ left | \ begin 2 0 4 \\ 6 -2 -1 \\ -4 2 5 \ end \ dreapta | = 0. $$

Din nou, minoră de ordinul trei fringing M_2 $ $, este egal cu zero. Deci, vom merge la un alt minor al treilea ordin. Ia minor de ordinul trei elemente se află la intersecția liniilor №1, №2, №3 și coloane №2, №3, №5. Acest minor este, de asemenea, marginita M_2 $ $:

$$ \ left | \ begin 2 0 5 \\ 6 -2 \\ -3 -4 2 7 \ end \ dreapta | = 4. $$

Astfel, printre minorii de ordinul trei mărginesc M_2 $ $, au minore, de zero, ceea ce implică $ \ sunat A≥ 3 $. Notam ca un minor M_3 $ $ non-zero. Elementele minore $ $ M_3 se află la intersecția liniilor de №1, №2, №3 și coloane №2, №3, №5. Devin tăiate minore $ $ M_3 minori ordinul patru. Pentru a începe cu vom lua ordinul al patrulea minor ale cărui elemente se află la intersecția liniilor №1, №2, №3, №4 și coloane №1, №2, №3, №5. Acest frontiere minore M_3 $ $. Valoarea sa nu este greu de găsit dacă utilizați, de exemplu, extinderea în rândul sau coloana:

$$ \ din stânga | \ începe 1 2 0 5 \\ 3 6 -2 -3 -2 \\ -4 2 7 \\ -1 -2 2 11 \ end \ dreapta | = 0. $$

În mod similar, având în vedere ordinul al patrulea minor ale cărui elemente sunt dispuse la intersecții de rânduri №1, №2, №3, №4 №2 și coloane, №3, №4, №5, obținem:

$$ \ left | \ begin 2 0 4 5 \\ 6 -2 -1 \\ -3 -4 2 5 7 \\ -2 2 9 11 \ end \ dreapta | = 0 $$.

Alte minori care mărginesc pentru minore $ $ M_3 nu. Toți minorii de un sfert de ordinul fringing M_3 $ $, egal cu zero. Ultimul nenulă minor, și anume $ $ M_3, a fost de trei ori. Concluzie: Rangul este 3, adică, $ \ A = 3 Rang $.

Găsiți Locul de $ matrice A = \ stânga (\ începe -1 3 2 4 1 \\ 0 -2 5 0 -3 \\ 1 -5 3 7 6 \ end \ dreapta) $ fringing de minori.

Din nou, începând cu decizia de selecție a doua ordine minore nu sunt egale cu zero. De exemplu, la intersecția liniilor №1, și coloane №1 nr.2, №2 sunt elemente minore \ $ din stânga | \ începe -1 3 \\ 0 -2 \ end \ dreapta | $, care se calculează folosind formula №1 a firelor cu privire la calculul determinanților al doilea și al treilea ordin:

Acest minor (notat cu $ M_2 $) nu este zero, prin urmare, că este ceea ce am devenit și tăiate minori de ordin al treilea. De exemplu, pentru a adăuga rânduri și coloane, pe care există elemente M_2 $ $, și mai mult linia №3 №3 coloanei. Ie găsi ordin al treilea minor, elementele care sunt situate la intersecția rândurilor №1, №2, №3 și coloane №1, №2, №3. Noi folosim formula №2 a firelor cu privire la calculul determinanților al doilea și al treilea ordin:

$$ \ left | \ începe -1 3 2 \\ 0 -2 5 \\ 1 -5 3 \ end \ dreapta | = 0. $$

Luați în considerare elementele minore de ordinul al treilea se află la intersecția liniilor №1, №2, №3 și coloane №1, №2, №4. Acest minor este, de asemenea, marginita M_2 $ $:

$$ \ left | \ începe -1 3 4 \\ 0 -2 0 \\ 1 -5 7 \ end \ dreapta | = 22. $$

Astfel, printre minorii de ordinul trei mărginesc M_2 $ $, există cel puțin un non-zero. Minorii forma a patra comandă nu mai putem, pentru liniile lor au nevoie de 4, iar în matricea $ A $ din toate cele 3 linii. Prin urmare, din moment ce acesta din urmă a fost nenul ordin al treilea minor, rangul este 3, adică, $ \ A = 3 Rang $.