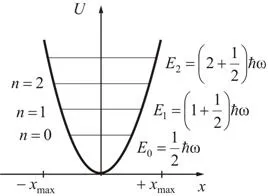
Armonica oscilator în mecanica cuantică

Acesta este independent de n. în contrast cu fântână pătrat, am considerat în Sec. 5.2.

Energia minimă se numește energia punctului zero. și anume când fluctuațiile atomilor în rețeaua cristalină Prin faptul că nu încetează.

În mecanica cuantică pentru a calcula probabilitatea diferitelor tranziții ale unui sistem cuantic de la un stat la altul. Pentru un oscilator armonic poate doar tranziții între nivelurile învecinate.

Condițiile impuse de schimbarea numerelor cuantice în tranzițiile de la un stat la altul, numit regulile de selecție. Pentru un oscilator armonic, în general, exprimată prin formula:

.

Din (5.3.4) implică faptul că energia cuantică a oscilatorului schimbă doar porțiuni, și anume cuantificată. Și, ca într-o gaură dreptunghiulară, de energie este limitată sub valoarea minimă

- energie (consecință directă a relației de incertitudine) de zero puncte. Aceasta înseamnă că o particulă nu poate fi în partea de jos a potențialului bine.

Densitatea de probabilitate de a găsi o particulă în Fig. 5.2. Ca și în cazul unui potențial bine dreptunghiular, cu n = 2, în mijlocul gropii nu poate fi o particulă. Este complet de neînțeles din punct de vedere clasic. Nu numai ca este energia cuantificată. dar coordonata particulei.

O particulă într-un bine unidimensional dreptunghiular trecerea particulelor printr-o barieră potențială. efect de tunel