Algoritmi pentru a găsi cea mai scurtă distanță în grafic

Titlul lucrării: algoritmi de căutare distanțe mai scurte într-un grafic

Specializarea: Informatică, Cibernetică și Programare

Descriere: A vrut să viziteze toate nodurile graficului și a reveni la vârful de pornire a minimiza costurile de călătorie și minimizarea timpului. Datele inițiale este grafic ale cărui arce sunt atribuite numere pozitive costurile de călătorie sau timpul necesar pentru a avansa de la un nod la altul. În general, graficul este orientată și la fiecare două vârfuri conecta două dintre arc înainte și înapoi. Să presupunem că doriți să găsiți distanța de la 1 la partea de sus a tuturor celorlalte.

Mărime fișier: 194.5 KB

Job descărcat: 18 persoane.

proiecție: algoritmi de căutare distanțe mai scurte într-un grafic Pagina 2 din 2

[2] Algoritmul de căutare mai scurte distanțe în coloana

[2.1] Dijkstra Algoritmul

[2.2] cea mai scurtă cale problemă

[2.3] problemă debit maxim

[2.4] Programarea liniară în timp ce maximizarea debitului

[3] de testare Întrebări

Graficele sunt utilizate pe scară largă atât în ​​matematică și aplicațiile sale. Acestea sunt utilizate în construcția de diferite modele matematice ale liniilor de transport, rețele de drumuri, linii de trafic aerian și așa mai departe.

Vreau să viziteze toate nodurile graficului și a reveni la magistrala p've de pornire, minimizând costurile de deplasare (sau a minimiza).

datele inițiale # 150; Acest grafic, care arce sunt atribuite numere pozitive # 150; costurile de călătorie sau timpul necesar pentru a avansa de la un nod la altul. În general, un ceai la grafic este orientat, și la fiecare două vârfuri sunt unite prin două arce # 150; înainte și înapoi. Într-adevăr, în cazul în care punctul A este situat pe munte, și punctul B # 150; în vale, în timp ce la perspectiva de plimbari de la A la B, în mod evident, mai puțin timp pe drumul de întoarcere de la B la A.

Multe producții de conținut economice sunt reduse la problema comis-voiajorului. De exemplu:

• a crea calea cea mai profitabilă de by-pass de reglare în magazin (controler, protecția și ka, ofițer de poliție), responsabil pentru buna funcționare a unui anumit set de obiecte (ka w dy acestor obiecte este modelat vârf al graficului);
• a crea calea cea mai favorabilă pentru piese sau hleboz pâine de lucru și apă pentru un anumit număr de brutării și alte puncte de vânzare cu amănuntul (parcare la brutărie).

Să luăm în considerare unele probleme tipice de luare a deciziilor legate de optimizarea pe grafice.

Algoritmul lui Dijkstra

Acest grafic algoritmi, inventat de E. Dijkstra. Ea găsește cea mai scurtă distanță de la unul dintre nodurile graficului tuturor celorlalte. Algoritmul funcționează numai pentru grafice fără margini greutate negativă. Algoritmul este utilizat pe scară largă în programarea și tehnologie, de exemplu, se utilizează protocolul OSPF pentru a elimina rutele circulare.

Să considerăm exemplul algoritmului graficului prezentat în Fig. Să presupunem că doriți să găsiți distanța de la 1 la partea de sus a tuturor celorlalte.

Cercurile reprezintă liniile nodurilor # 151; căi între ele (muchiile graficului). Cercul indică numărul de noduri pe marginile indicate de „preț“ lor # 151; lungimea căii. Pe lângă fiecare nod indicat printr-un marcaj roșu # 151; lungimea cea mai scurtă cale în vârful nod 1.

Primul pas. Luați în considerare algoritmul pas Dijkstra pentru acest exemplu. Nota minimă are un nod 1. vecinii săi sunt la vârf 2, 3 și 6.

Primul de un vecin nod 1 # 151; Vertex 2, deoarece lungimea calea este minimă. Lungimea în ea prin partea de sus 1 este egală cu distanța cea mai scurtă până la marginea superioară 1 + lungime mergând de la 1 la 2, și anume, 0 + 7 = 7. Acest lucru este mai mică decât etichetele nodurilor curente 2, astfel încât noua etichetă a 2 vârfuri este 7.

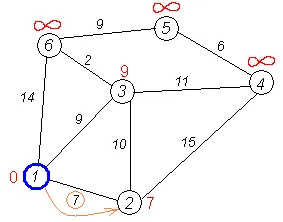
Noi facem aceeași operațiune cu celelalte doi vecini ai primul Vertex # 151; 3 și 6-a.

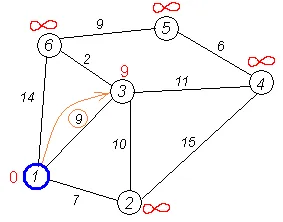
Toți vecinii sunt de top 1 verificate. Distanța minimă curent la partea de sus 1 sunt definitive și nu fac obiectul unui recurs (faptul că acest lucru este atât, pentru prima dată, sa dovedit Dijkstra). Noi șterge din grafic. Trebuie remarcat faptul că vârful a avut.

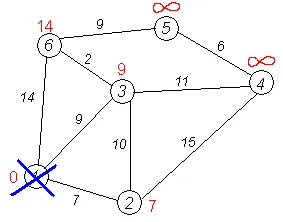
Al doilea pas. Etapa a algoritmului se repetă. Din nou vom găsi „cel mai apropiat“ de noduri nu au fost vizitate. Acest vertex 2 Tagged 7.

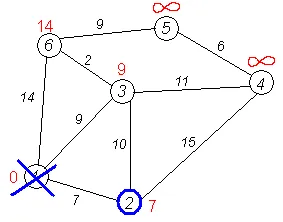
Din nou, încercăm să reducem etichetele vecine selectate nod, încercând să-i prin intermediul a 2-a. Vecinii vertex 2 sunt 1, 3, 4.

Primul (în ordine) un nod vecin 2 # 151; nod 1. Dar ea deja a avut, asa ca de la primul nod nu fac nimic.

Vecinul vertex 2 # 151; 3. În cazul în care vârful să-l păstrați la 2, atunci lungimea unui astfel de cale ar fi 7 + 10 = = 17. Dar marca de curent este egal cu al treilea vârful 9<17, поэтому метка не меняется.

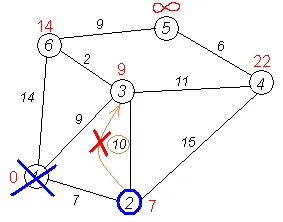
Un alt vecin vertex 2 # 151; 4. Dacă vârful pentru a intra în ea prin 2-a, atunci lungimea acestei căi este cea mai scurtă distanță = 2 + distanța între nodurile 2 și 4 = 7 + 15 = 22. Deoarece 22<. устанавливаем метку вершины 4 равной 22.

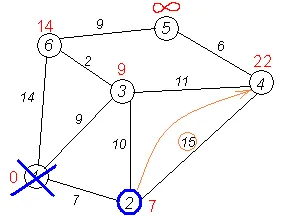
Al treilea pas. Repetați acest pas al algoritmului de sus 3. După ce sa „prelucrare“ vom obține următoarele rezultate:

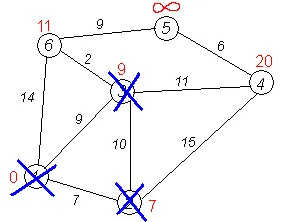
Pașii următori. Algoritmul repetă etapa pentru nodurile rămase (Va fi pe ordinea de 6, 4 și 5).

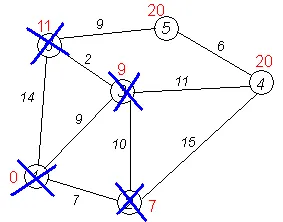
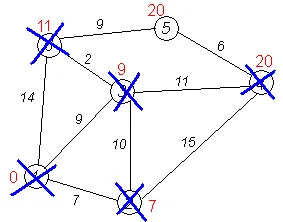
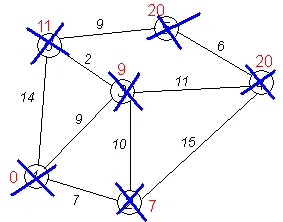
Finalizarea algoritmului. Algoritmul se termină atunci când toate nodurile sunt șterse. Rezultatul muncii sale este văzut în ultima figură: calea cea mai scurtă de la partea de sus 1 la 2 minute se numără 7 3 minute # 151; 9 la 4-lea # 151; 20, 5 th # 151; 20, 6 th # 151; 11.

Cea mai scurtă cale problemă

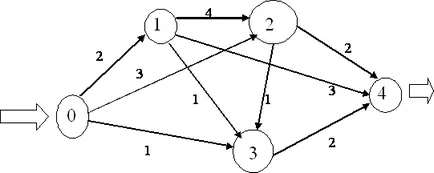
Ca cel mai scurt drum pentru a ajunge de la un nod la altul? În ceea ce privește managementul producției: modul în care cel mai scurt drum (și, în consecință, cu cel mai mic consum de combustibil și de timp, cel mai ieftin) pentru a obține de la punctul A la punctul B? Pentru a rezolva această problemă, fiecare arc de un grafic direcționat ar trebui să fie comparat cu numărul de # 150; timpul de mișcare a arcului din nodul inițial la un final. Să considerăm exemplul (Figura 7).

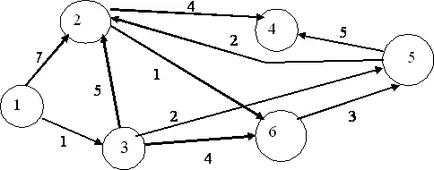
Figura 7. Contextul cea mai scurtă cale de problema.

Situația poate fi descrisă nu numai grafic direcționat cu greutăți, atribuite arce, dar, de asemenea, un tabel (Tabelul 8).

Tabelul 8. Contextul cea mai scurtă cale de problema.

Provocarea: cum să obțineți cea mai scurtă cale de la vârf 1 în top 4?

Decizie. Noi introducem notația C (T) # 150; lungimea cea mai scurtă cale de la un nod la T. vertex Deoarece orice cale pe care trebuie să ia în considerare este format din arce și arcele unui număr finit, și fiecare conține nu mai mult de o dată, reclamantele pentru un număr finit de calea cea mai scurtă, și cel puțin un număr finit de elemente întotdeauna realizat. Problema în discuție constă în calcularea C (4), și prevede modalități prin care se atinge acest minim.

Pentru datele inițiale prezentate în Figura 7 și în tabelul 6, în partea superioară 3 este doar o săgeată, doar din partea de sus și aproximativ 1. Această săgeată este lungimea sa, care este egal cu 1. Prin urmare, C (3) = 1. Mai mult, este evident că G (1) = 0. 4 de sus poate fi accesat fie din calea superioară 2. trecere egală cu 4 sau 5 din partea de sus, după ce trece o cale egală cu 5. Prin urmare, relația C (4) = min.

Astfel, sarcina restructurate # 150; determinarea C (4) se reduce la determinarea C (2) și C (5). Top 5 poate fi accesat din partea de sus calea 3. trecere egală cu 2, sau de la calea de trecere la vârf 6. egal cu 3. Prin urmare, relația C (5) = min. Știm că C (3) = 1. Prin urmare, C (5) = min. Deoarece este evident că C (6) # 150; număr pozitiv, ultima relație rezultă că C (5 = 3. În primii 2 se poate ajunge la oricare nod 1, având o cale egală sau din vertex 7. calea 3. trecere egală cu 5. 5. fie din partea de sus, după ce trece calea egal cu 2. Prin urmare, relația C (2) = min. ştim că C (1) = 0, C (3 = 1, C (5) = 3. Prin urmare, C (2) = min = 5.

Astfel, lungimea cea mai scurtă cale este 8. Din această relație este clar că în top 4 pentru a merge prin top 5. Revenind la calculul C (5), vom vedea că vârful 5 pentru a trece prin partea de sus 3. În top 3 se poate obține numai 1 din Vertex.

Astfel, cea mai scurtă rută este după cum urmează: 1 → 3 → 5 → 4.

Shortest problemă cale pentru datele de intrare specifice (Figura 7 și Tabelul 6) este pe deplin rezolvată.

Probleme de optimizare pe grafice care apar în pregătirea deciziilor de management în managementul producției, sunt foarte diverse. De exemplu, ia în considerare mai mult de o problemă legată de transport.

problemă maximă de curgere

Traseul pe care să trimită numărul maxim posibil de mărfuri din punctul de plecare până la destinația finală în cazul în care căile de lățime de bandă între punctele este limitat?

Pentru a rezolva această problemă, fiecare arc de un grafic direcționat, sistemul de transport corespunzător trebuie să fie mapat la numărul - capacitatea arcului. Să considerăm exemplul (Figura 8).

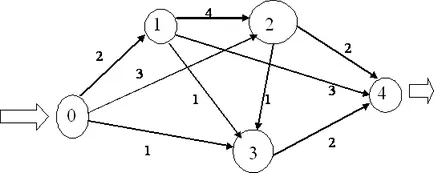
Figura 8. Contextul problema maximă de curgere

Datele inițiale privind sistemul de transport, de exemplu, în plante prezentate în Figura 8, pot fi de asemenea setat tabel (tabelul 9).

Tabelul 9. Contextul problema maximă de curgere

Decizia cu privire la problema maximă de curgere poate fi obținută din următoarele considerente.

Evident, capacitatea maximă de transport a sistemului este mai mic de 6, deoarece nu mai mult de 6 unități de mărfuri pot fi trimise de la punctul inițial 0, și anume, unitățile 2, alineatul 1, Unitatea 3, alineatul 2, și 1 unitate de la punctul 3.

În plus, este necesar să se asigure că toate 6 ieșit de la 0 unități de marfă a ajuns la destinație 4. Evident, 2 unități de marfă, care a venit la alineatul 1, pot fi trimise direct la etapa 4. A venit la punctul 2 sarcini trebuie să împartă: trimite 2 unități imediat elementul 4, și 1 unitate # 150; 3 într-un punct intermediar (datorită porțiunii limitate a capacității de transfer între punctele 2 și 4). La punctul 3, livrate astfel de bunuri: 1 unitate de la 0 și 1 unitate de produs 3. Acestea sunt menționate la punctul 4.

Astfel, capacitatea maximă a sistemului de transport considerat # 150; 6 unități de marfă. Ea nu utilizează porțiuni interioare (sucursale) între punctele 1 și 2, precum și între punctele 1 și 3. puncte de ramificare dogruzhena între 1 și 4 # 150; Acesta sa axat pe două unități de marfă cu capacitatea de 3 unități.

Soluția poate fi reprezentată ca un tabel (Tabelul 10)

Tabelul 10. Decizia cu privire la problema maximă de curgere

problemă de programare liniară în timp ce maximizarea debitului

Noi oferim o formulare de probleme de curgere maximă în ceea ce privește programarea liniară. Fie X KM # 150; volumul de trafic de la punctul K punctul M. Prin Fig.8 K = 0,1,2,3, M = 1,2,3,4, și de transport posibile numai la punctul cu un număr mare. Deci, toate sunt 9 variabile X KM. și anume, X 01 X 02 X 03 X 12 X 13 X 14 X 23 X 24 X 34. Problema programării liniare, având ca scop maximizarea fluxului este dată de: F → max.

X 01 X + 02 + 03 X = F (0)
- X 01 + 12 + X + X 13 X 14 = 0 (1)
- X 02 - 12 X + X + 23 X 24 = 0 (2)
-X 03 X 13 X 23 X + 34 = 0 (3)
-X 14 X 24 X 34 = -F (4)
≤ 2 X 01

X KM ≥ 0. Pentru M = 0, F ≥ 0, 1, 2, 3, 4.

aici F # 150; Funcția obiectiv, condiție (0) descrie intrarea mărfurilor în sistemul de transport. Condiția (1) # 150; (3) definesc raportul echilibru pentru nodurile # 1 sistem 150 3. Cu alte cuvinte, pentru fiecare dintre nodurile interne de intrare este fluxul de bunuri sarcini efluentului și nu se acumulează în interiorul sistemului, și nu „născut“ în aceasta. Condiții (4) # 150; Această condiție de „ieșire“ din sistemul de marfă. Împreună cu condiția (0), constituie raportul de echilibru pentru sistem ca întreg ( „intrare“ este „ieșire“). Următoarele nouă inegalități stabilite limite privind capacitatea individului „ramuri“ ale sistemului de transport. Apoi specificați non-negativitate a volumelor de trafic și funcția obiectiv.

Este clar că ultima inegalitate rezultă din forma funcției obiectiv (relația (0) sau (4)) și volumele de trafic non-negativitate. Cu toate acestea, această inegalitate are unele informații generale # 150; prin intermediul sistemului poate fi omisă sau o valoare pozitivă de mărfuri, sau zero (de exemplu, dacă în sistem există o mișcare într-un cerc), dar nu și negativ (nu are nici un sens economic, ci un model matematic formale nu „știe“ despre el).

1. Definiți algoritmul de căutare în grafice.
2. Principiul de funcționare al algoritmului lui Dijkstra.
3. Pentru a formula problema calea cea mai scurtă. Domeniu de aplicare.
4. Formulați o problemă de curgere maximă. Domeniu de aplicare.
5. Formulați o problemă de programare liniară în timp ce maximizarea debitului. Domeniu de aplicare.

Tsentralnі ponyattya doslіdzhennya prognozuvannya principal parametrіv dіyalnostі organіzatsії. Suchasnі naukovі pіdhodi la rozumіnnya prognozuvannya principal Parametrіv dіyalnostі organіzatsії PROGNOZUVANNYA principal PARAMETRІV DІYALNOSTІ ORGANІZATSІЇ În SISTEMІ MANAGEMENT Suchasnyj PІDPRIЄMSTVA. Prognozuvannya în sistemі pіdpriєmstva managementul strategіchnogo.

Romanenko Kursova robotului Ekonomichna efektivnіst virobnitstva rіpaku i Drumuri Ahead її pіdvischennya Student vіddіlennya Ekonomіka pіdpriєmstva Naukovі Fundamentele pіdvischennya ekonomіchnoї efektivnostі virobnitstva rіpaku. Pokazniki ekonomіchnoї efektivnostі virobnitstva rіpaku că tehnica їh viznachennya. Rіven virobnitstva rіpaku că Yogo Ekonomichna efektivnіst.